题目内容
4.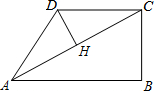 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )| A. |  | B. |  | C. | 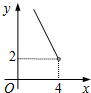 | D. | 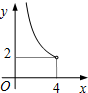 |
分析 由△DAH∽△CAB,得$\frac{AD}{AC}$=$\frac{AH}{AB}$,求出y与x关系,再确定x的取值范围即可解决问题.
解答  解:∵DH垂直平分AC,
解:∵DH垂直平分AC,
∴DA=DC,AH=HC=2,
∴∠DAC=∠DCH,
∵CD∥AB,
∴∠DCA=∠BAC,
∴∠DAH=∠BAC,∵∠DHA=∠B=90°,
∴△DAH∽△CAB,
∴$\frac{AD}{AC}$=$\frac{AH}{AB}$,
∴$\frac{y}{4}$=$\frac{2}{x}$,
∴y=$\frac{8}{x}$,
∵AB<AC,
∴x<4,
∴图象是D.
故选D.
点评 本题科学相似三角形的判定和性质、相等垂直平分线性质、反比例函数等知识,解题的关键是正确寻找相似三角形,构建函数关系,注意自变量的取值范围的确定,属于中考常考题型.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
18. 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{6}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{3}{13}$ |
13.菱形ABCD中,对角线AC、BD相交于O,H为AD边中点,OH的长等于3,则菱形ABCD的周长为( )
| A. | 24 | B. | 12 | C. | 9 | D. | 18 |
9.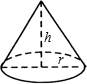 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )
如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )
 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )
如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )| A. | 30πcm2 | B. | 48πcm2 | C. | 60πcm2 | D. | 80πcm2 |
 如图,已知直线l1:y=0.5x+3和l2:y=mx+n交于点P(-1,a),且l1和l2分别与y轴交于点A、B,与x轴交于点C、D,根据以上信息解答下问题:
如图,已知直线l1:y=0.5x+3和l2:y=mx+n交于点P(-1,a),且l1和l2分别与y轴交于点A、B,与x轴交于点C、D,根据以上信息解答下问题:

 如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )