题目内容
4.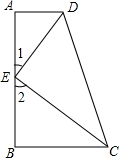 如图所示,AD⊥AB,DE,CE分别是∠ADC与∠BCD的平分线,∠1+∠2=90°,AD与BC平行吗?为什么?
如图所示,AD⊥AB,DE,CE分别是∠ADC与∠BCD的平分线,∠1+∠2=90°,AD与BC平行吗?为什么?
分析 AD与BC平行.通过“同旁内角互补,两直线平行”来证明AD与BC平行.
解答  解:平行,理由如下:
解:平行,理由如下:
∵∠1+∠2=90°,
∴∠DEC=90°,
∴∠4+∠5=90°.
∵DE,CE分别平分∠ADC,∠BCD,
∴∠ADC=2∠4,∠DCB=2∠5,
∠ADC+∠DCB=2(∠4+∠5)=180°,
∴AD∥BC,即AD与BC平行.
点评 本题考查了平行线的判定.此题利用三角形内角和定理和平角的定义求得∠4+∠5=90°是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
12.有一组数据:3,4,5,6,6,则这组数据的平均数、众数、中位数分别是( )
| A. | 4.8,6,5 | B. | 5,5,5 | C. | 4.8,6,6 | D. | 5,6,5 |
19.若$\frac{x+y}{y}=\frac{7}{4}$,那么$\frac{y}{x}$的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
9.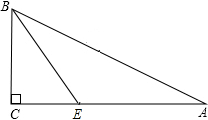 如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
 如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )| A. | 3 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
14.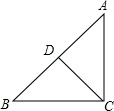 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )| A. | ∠ACD=∠B | B. | ∠ADC=∠ACB | C. | AC2=AD•AB | D. | BC2=BD•BA |
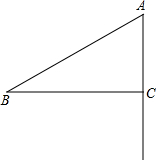 如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点D从点A出发,以每秒1cm的速度沿射线AC运动,当t=5、6、$\frac{25}{6}$时,△ABD为等腰三角形.
如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点D从点A出发,以每秒1cm的速度沿射线AC运动,当t=5、6、$\frac{25}{6}$时,△ABD为等腰三角形. Φ
Φ 如图,AD是△ABC的中线,E是AD的中点,BE的延长线交AC于点F,若FC=12,AF的长为( )
如图,AD是△ABC的中线,E是AD的中点,BE的延长线交AC于点F,若FC=12,AF的长为( )