题目内容
19.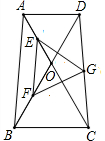 在梯形ABCD中,AD∥BC,AB=CD,∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由.
在梯形ABCD中,AD∥BC,AB=CD,∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由.
分析 如图,作辅助线;首先证明∠OAD=∠ODA,得到AO=DO,结合∠AOD=60°,判断出△AOD为等边三角形,此为解题的关键性结论;其次证明DE⊥AC,运用直角三角形的性质证明EG=FG=$\frac{1}{2}CD$;运用三角形的中位线定理证明EF=$\frac{1}{2}$AB,结合AB=CD,得到EG=FG=EF,即可解决问题.
解答  解:△EFG为等边三角形;证明如下:
解:△EFG为等边三角形;证明如下:
如图,连接DE、CF;
∵AD∥BC,AB=CD,
∴四边形ABCD为等腰梯形,
∴AC=BD;
在△ABD与△DCA中,
$\left\{\begin{array}{l}{AB=DC}\\{AD=DA}\\{BD=AC}\end{array}\right.$,
∴△ABD≌△DCA(SSS),
∴∠OAD=∠ODA,AO=DO;而∠AOD=60°,
∴△AOD为等边三角形,AD=OD;
∵AE=OE,
∴DE⊥AO,△CDE为直角三角形,
∵DG=CG,
∴EG=$\frac{1}{2}$CD;同理可求:FG=$\frac{1}{2}$CD;
∵E为OA的中点,F为OB的中点,
∴EF为△OAB的中位线,
∴EF=$\frac{1}{2}$AB;而AB=CD,
∴EG=FG=EF,
∴△EFG为等边三角形.
点评 该题主要考查了等腰梯形的性质、全等三角形的判定、等边三角形的判定、三角形的中位线定理等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用全等三角形的判定、三角形的中位线定理等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
9.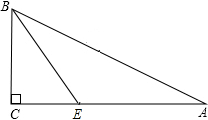 如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
 如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )
如图所示,在三角形纸片ABC中,∠C=90°,∠A=30°,AB=12,BE平分∠ABC,则AE的长度为( )| A. | 3 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
14.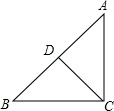 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )| A. | ∠ACD=∠B | B. | ∠ADC=∠ACB | C. | AC2=AD•AB | D. | BC2=BD•BA |
4.用分数表示(-2)-2,正确的是( )
| A. | $\frac{1}{{2}^{-2}}$ | B. | -$\frac{1}{{2}^{2}}$ | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
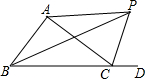 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°.