题目内容
有个底角为60°,周长为40的等腰梯形,它的最大面积为( )
| A、20 | ||
B、50
| ||
| C、100 | ||
D、8
|
考点:等腰梯形的性质
专题:
分析:根据题意作BE⊥AB,在Rt△ABE中,求出BE=
AB,设出AB=x,梯形的面积为S,利用梯形的周长可得出AD+BC的值,代入梯形面积公式即可得出S与x的函数表达式.根据等腰梯形的性质可求得梯形的高,再根据面积公式可列出用x表示梯形面积的函数关系式,找出其顶点即可求得腰为多长时的面积最大.
| ||
| 2 |
解答: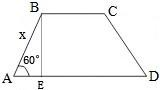 解:如图所示,作BE⊥AB.
解:如图所示,作BE⊥AB.
在Rt△ABE中,∠A=60°,
设AB=x,梯形的面积为S,则BE=
AB=
x,
∵四边形ABCD是等腰梯形,
∴AD+BC=40-AB-CD=40-2x,
梯形的面积S=
(AD+BC)×BE=
×(40-2x)×
x=-
x2+10
x=-
(x-10)2+50
(0<x<40),
∴该抛物线的顶点坐标为(10,50
),
即这个梯形的最大面积为50
.
故选B.
 解:如图所示,作BE⊥AB.
解:如图所示,作BE⊥AB.在Rt△ABE中,∠A=60°,
设AB=x,梯形的面积为S,则BE=
| ||
| 2 |
| ||
| 2 |
∵四边形ABCD是等腰梯形,
∴AD+BC=40-AB-CD=40-2x,
梯形的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
∴该抛物线的顶点坐标为(10,50
| 3 |
即这个梯形的最大面积为50
| 3 |
故选B.
点评:该题考查了根据实际问题抽象二次函数关系式的知识,掌握梯形的面积公式及等腰梯形的性质是解答本题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图是将长方形纸片沿对角线折叠得到的,图中(包括实线、虚线在内) 共有全等三角形( )对.
如图是将长方形纸片沿对角线折叠得到的,图中(包括实线、虚线在内) 共有全等三角形( )对.| A、2 | B、3 | C、4 | D、5 |
 已知点B、C分别在∠MAN的两边上,BD⊥AM,CE⊥AN,垂足分别为D、E,BD、CE相交于点F,且BF=CF,试说明点F在∠A的平分线上.
已知点B、C分别在∠MAN的两边上,BD⊥AM,CE⊥AN,垂足分别为D、E,BD、CE相交于点F,且BF=CF,试说明点F在∠A的平分线上. 如图,AB是圆O的直径,C是圆O上一点,∠ABC的平分线交圆O于E,交AC于D,过E作AC的平行线,交BA的延长线于F.试探索AE,CD,EF线段的关系.
如图,AB是圆O的直径,C是圆O上一点,∠ABC的平分线交圆O于E,交AC于D,过E作AC的平行线,交BA的延长线于F.试探索AE,CD,EF线段的关系.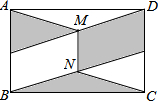 如图,在矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3,BC=2
如图,在矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3,BC=2