题目内容
已知△ABC的三边长分别为6，10，8，则△ABC的面积为（ ）
| A、24 | B、48 |
| C、30 | D、不能确定 |
考点：勾股定理的逆定理
专题：
分析：根据三边长度可利用勾股定理逆定理判断三角形为直角三角形．再求面积．
解答：解：∵△ABC的三边分别为6，10，8，
且62+82=102，
∴△ABC是直角三角形，两直角边是6，8，
∴△ABC的面积为：
×6×8=24，
故选：A．
且62+82=102，
∴△ABC是直角三角形，两直角边是6，8，
∴△ABC的面积为：
| 1 |
| 2 |
故选：A．
点评：本题主要考查了勾股定理的逆定理和直角三角形的面积公式，关键是掌握如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
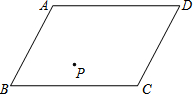解决问题：有兄弟俩分家时，原来共同承包的一块平行四边形田地ABCD，现要进行平均划分，由于在这块地里有一口水井P，如图所示，为了兄弟俩都能方便使用这口井，兄弟俩在划分时犯难了．聪明的你能帮他们解决这个问题吗？
化简二次根式：a
，结果正确的是（ ）
-
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|