题目内容
．
解：原方程组化简为：
①×2+②×3得：8x-6y+9x+6y=24+27，
即17x=51，解得x=3，
把x=3代入②得：3×3+2y=9，解得y=0，
所以原方程组的解为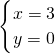
．
分析：把原方程组中的第一个方程左右两边同时乘以12，去分母后记作①，第二个方程记作②，联立①②构成新的方程组，根据①×2+②×3，消去y后得到关于x的一元一次方程，求出方程的解得到x的值，将求出的x的值代入②即可求出y的值，进而得到方程组的解．
点评：此题考查了二元一次方程组的解法，其解法有两种：加减法和代入法，无论哪种方法解二元一次方程组，其思想都是“消元”．此外注意二元一次方程组解得写法，即求出解后，联立求出的x与y．
①×2+②×3得：8x-6y+9x+6y=24+27，
即17x=51，解得x=3，
把x=3代入②得：3×3+2y=9，解得y=0，
所以原方程组的解为
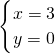．分析：把原方程组中的第一个方程左右两边同时乘以12，去分母后记作①，第二个方程记作②，联立①②构成新的方程组，根据①×2+②×3，消去y后得到关于x的一元一次方程，求出方程的解得到x的值，将求出的x的值代入②即可求出y的值，进而得到方程组的解．
点评：此题考查了二元一次方程组的解法，其解法有两种：加减法和代入法，无论哪种方法解二元一次方程组，其思想都是“消元”．此外注意二元一次方程组解得写法，即求出解后，联立求出的x与y．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
，求这个函数的解析式；
是同类二次根式的是
如图，△ABC中，∠C=90°，CD⊥AB，BD=8，AD=2，则tanA=
已知：如图，E、F分别是正方形ABCD的边BC、CD上的点，AE、AF分别与对角线BD相交于M、N，若∠EAF=50°，则∠CME+∠CNF=________度．
和直线y=-x+8的一个交点，设点A的坐标为（a，b），则
=________．