题目内容
 已知:如图,E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF=________度.
已知:如图,E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF=________度.
100
分析:先证明△CMN≌△AMN,得到∠AMC+∠ANC=360°-50°-50°=260°,根据角和补角和为180°可以解本题.
解答: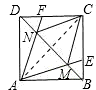 解:连接AC,
解:连接AC,
则AC所在直线为BD的垂直平分线,
∴AM=AN=CM=CN,
在△AMN和△CMN中, ,
,
∴△AMN≌△CMN,即∠EAF=∠MCN=50°
∴∠AMC+∠ANC=360°-50°-50°=260°,
∵∠CNF=180°-∠ANC,
∠CME=180°-∠CMA,
∴∠CME+∠CNF=180°-∠CMA+180°-∠ANC=100°
故答案为 100.
点评:本题考查了全等三角形的判定,考查了正方形对角线互相平分的性质,考查了四边形内角和为360°的性质,本题中求证△AMN≌△CMN是解题的关键.
分析:先证明△CMN≌△AMN,得到∠AMC+∠ANC=360°-50°-50°=260°,根据角和补角和为180°可以解本题.
解答:
 解:连接AC,
解:连接AC,则AC所在直线为BD的垂直平分线,
∴AM=AN=CM=CN,
在△AMN和△CMN中,
 ,
,∴△AMN≌△CMN,即∠EAF=∠MCN=50°
∴∠AMC+∠ANC=360°-50°-50°=260°,
∵∠CNF=180°-∠ANC,
∠CME=180°-∠CMA,
∴∠CME+∠CNF=180°-∠CMA+180°-∠ANC=100°
故答案为 100.
点评:本题考查了全等三角形的判定,考查了正方形对角线互相平分的性质,考查了四边形内角和为360°的性质,本题中求证△AMN≌△CMN是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
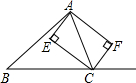 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F. 21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.
21、已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点.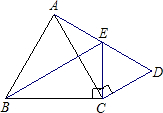 已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形.
已知:如图,△BCE、△ACD分别是以BE、AD为斜边的直角三角形,且BE=AD,△CDE是等边三角形.求证:△ABC是等边三角形. 已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE.
已知:如图,E,F分别是?ABCD的边AD,BC的中点.求证:AF=CE. 已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.
已知,如图,BE、CF分别是△ABC的边AC、AB上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.请你判断线段AD与AG有什么关系?并证明.