题目内容
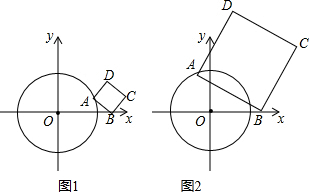
如图1,已知⊙O的半径为
,正方形ABCD的顶点B的坐标为(2,0),顶点A在⊙O上运动,顶点C在x轴上方.
(1)当点A在x轴上时,求点C的坐标;
(2)点A在运动过程中,是否存在直线AB与⊙O相切的位置关系?若存在,请求出点C的坐标,若不存在,请说明理由.
(3)如图2,当点A运动到第二象限时,设AB交⊙O于点P,当sin∠CBX=
时,求弦AP的长.
| 3 |
(1)当点A在x轴上时,求点C的坐标;
(2)点A在运动过程中,是否存在直线AB与⊙O相切的位置关系?若存在,请求出点C的坐标,若不存在,请说明理由.
(3)如图2,当点A运动到第二象限时,设AB交⊙O于点P,当sin∠CBX=
| 3 |
| 4 |

考点:圆的综合题
专题:
分析:(1)利用A点在y轴右侧或左侧分别分析得出即可;
(2)利用已知C点在x轴上方,符合题意的只有一种情况,再利用锐角三角函数关系求出FO、FC的长进而得出答案;
(3)利用sin∠CBX=
,得出sin∠MOB=
,进而求出OM,MP的长,进而得出答案.
(2)利用已知C点在x轴上方,符合题意的只有一种情况,再利用锐角三角函数关系求出FO、FC的长进而得出答案;
(3)利用sin∠CBX=
| 3 |
| 4 |
| 3 |
| 4 |
解答: 解:(1)如图1,∵⊙O的半径为
解:(1)如图1,∵⊙O的半径为
,正方形ABCD的顶点B的坐标为(2,0),
∴当点A在x轴上时,BO=2,BC=2-
,
∴点C(2,2-
)
如图2,∵⊙O的半径为
,正方形ABCD的顶点B的坐标为(2,0),
∴当点A在x轴上时,BO=2,AB=BC=2+
,
∴点C(2,2+
)
综上所述:C(2,2-
)或(2,2+
);
(2)如图3,
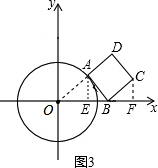
当直线AB与⊙O相切于点A,过点A作AE⊥OB于点E,过点C作CF⊥OB于点F,
则∠OAB=90°,
∵BO=2,AO=
,
∴AB=1,
∴∠AOE=30°,
∴AE=
,
∴BE=
,
∴∠ABE=60°,
∴∠CBF=30°,
∴FC=
,BF=
,
∴FO=2+
,
∴C (2+
,
);
(3)如图4,

作OM⊥AB于M,连结OP.
∵OM∥BC,
∴∠MOB=∠CBx.
又∵sin∠CBx=
,
∴sin∠MOB=
.
∵OB=2,
∴BM=
,
∴OM=
=
.
又∵OP=
,
∴MP=
=
,
∴AP=2MP=
.
 解:(1)如图1,∵⊙O的半径为
解:(1)如图1,∵⊙O的半径为| 3 |
∴当点A在x轴上时,BO=2,BC=2-
| 3 |
∴点C(2,2-
| 3 |
如图2,∵⊙O的半径为
| 3 |
∴当点A在x轴上时,BO=2,AB=BC=2+
| 3 |
∴点C(2,2+
| 3 |
综上所述:C(2,2-
| 3 |
| 3 |
(2)如图3,

当直线AB与⊙O相切于点A,过点A作AE⊥OB于点E,过点C作CF⊥OB于点F,
则∠OAB=90°,
∵BO=2,AO=
| 3 |
∴AB=1,
∴∠AOE=30°,
∴AE=
| ||
| 2 |
∴BE=
| 1 |
| 2 |
∴∠ABE=60°,
∴∠CBF=30°,
∴FC=
| 1 |
| 2 |
| ||
| 2 |
∴FO=2+
| ||
| 2 |
∴C (2+
| ||
| 2 |
| 1 |
| 2 |
(3)如图4,

作OM⊥AB于M,连结OP.
∵OM∥BC,
∴∠MOB=∠CBx.
又∵sin∠CBx=
| 3 |
| 4 |
∴sin∠MOB=
| 3 |
| 4 |
∵OB=2,
∴BM=
| 3 |
| 2 |
∴OM=
| OB2-BM2 |
| ||
| 2 |
又∵OP=
| 3 |
∴MP=
| OP2-OM2 |
| ||
| 2 |
∴AP=2MP=
| 5 |
点评:此题主要考查了圆的综合应用以及锐角三角函数关系和勾股定理等知识,动态问题,综合性较强,凸现对学生的运动探究、问题解决能力的考查.问题简洁且清新扑面,消除学生解最后一题的恐惧心理.增加学生的参与面,能力立意,全新创作,揭示数学学习的本质,不必搞题海战术.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,?ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF,求证:四边形BFDE是平行四边形.
如图,?ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF,求证:四边形BFDE是平行四边形.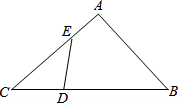 已知:如图,△ABC中,点D、E分别是BC、AC边上的点,且BC:DC=3:1,∠B=∠CED,BC=12,AC=8.
已知:如图,△ABC中,点D、E分别是BC、AC边上的点,且BC:DC=3:1,∠B=∠CED,BC=12,AC=8.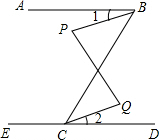 如图,已知∠P=∠Q,∠1=∠2,AB与ED平行吗?为什么?
如图,已知∠P=∠Q,∠1=∠2,AB与ED平行吗?为什么? 如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点.
如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点. 在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠A=∠D=90°,AB=BC=15千米,CD=3
在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠A=∠D=90°,AB=BC=15千米,CD=3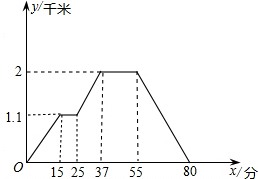 如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:
如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题: 如图,在△ABC中,AC=BC,∠B=70°,分别以点A、C为圆心,大于
如图,在△ABC中,AC=BC,∠B=70°,分别以点A、C为圆心,大于