题目内容
9.已知∠ABC=90°,D是直线AB上的点,AD=BC,E是直线BC上的一点,直线AE、CD相交于点P,且∠APD=45°,当点D、E分别在AB、AC上时,如图(1),易证:BD=CE.当点D在AB延长线上,点E在BC延长线上时,如图(2);当点D在AB反向延长线上,点E在BC延长线上时,如图(3).图(2)图(3)又有怎样的结论?猜想并选择其中一图进行证明.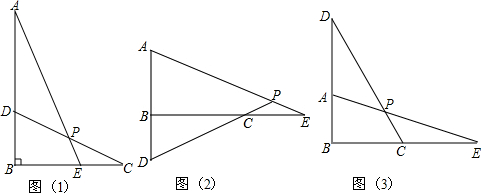
分析 图(2)中,结论:BD=CE,由△FAD≌△DBC得DF=DC,可以证明△DFC是等腰直角三角形,再证明四边形AECF是平行四边形,即可解决问题,图(3)结论不变,证明方法类似.
解答 解:图(2)中,结论:BD=CE
理由:作AF⊥AB于A,使AF=BD,连结DF,CF,
∴∠FAD=90°.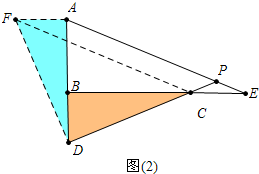
∵∠B=90°,
∴∠FAD=∠B,
在△FAD和△DBC中,
$\left\{\begin{array}{l}{AF=BD}\\{∠FAD=∠B}\\{AD=BC}\end{array}\right.$,
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD,
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°,
∵∠APD=45°,
∴∠FCD=∠APD,
∴FC∥AP,
∵∠FAD=90°,∠ABC=90,
∴∠FAD=∠ABC,
∴AF∥BC.
∴四边形AECF是平行四边形,
∴AF=CE,∵AF=BD
∴BD=CE.
(2)图(3)中,结论:BD=CE
理由:作AF⊥AB于A,使AF=BD,连结DF,CF,
∴∠FAD=90°.
∵∠B=90°,
∴∠FAD=∠B,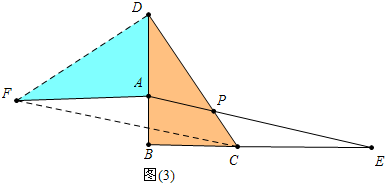
在△FAD和△DBC中,
$\left\{\begin{array}{l}{AF=BD}\\{∠FAD=∠B}\\{AD=BC}\end{array}\right.$,
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD,
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°,
∵∠APD=45°,
∴∠FCD=∠APD,
∴FC∥AP,
∵∠FAD=90°,∠ABC=90,
∴∠FAD=∠ABC,
∴AF∥BC.
∴四边形AECF是平行四边形,
∴AF=CE,∵AF=BD,
∴BD=CE.
点评 此题考查了全等三角形的判定与性质/平行四边形的判定及性质/等腰直角三角形的判定及性质,添加辅助线构造全等三角形是解题的关键,属于中考常考题型.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案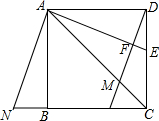 已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.
已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.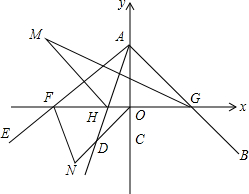 如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.
如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.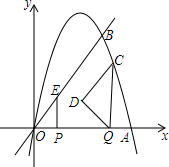 如图,抛物线y=-x2+6x与x轴交于O,A两点,与直线y=2x交于O,B两点.点P在线段OA上以每秒1个单位的速度从点O向终点A运动,作EP⊥x轴交直线OB于E;同时在线段OA上有另一个动点Q,以每秒1个单位的速度从点A向点O运动(不与点O重合).作CQ⊥x轴交抛物线于点C,以线段CQ为斜边作如图所示的等腰直角△CQD.设运动时间为t秒.
如图,抛物线y=-x2+6x与x轴交于O,A两点,与直线y=2x交于O,B两点.点P在线段OA上以每秒1个单位的速度从点O向终点A运动,作EP⊥x轴交直线OB于E;同时在线段OA上有另一个动点Q,以每秒1个单位的速度从点A向点O运动(不与点O重合).作CQ⊥x轴交抛物线于点C,以线段CQ为斜边作如图所示的等腰直角△CQD.设运动时间为t秒.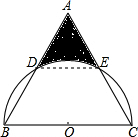 如图,在边长为2的等边△ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则图中阴影部分的面积是(结果保留π)$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,在边长为2的等边△ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则图中阴影部分的面积是(结果保留π)$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.