题目内容
19.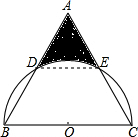 如图,在边长为2的等边△ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则图中阴影部分的面积是(结果保留π)$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,在边长为2的等边△ABC中,以BC为直径的半圆分别交AB、AC于点D、E,则图中阴影部分的面积是(结果保留π)$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
分析 连接OD,OE,则四边形ODEC是菱形,菱形的面积减去扇形DOE的面积即可求解.
解答 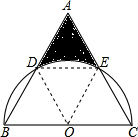 解:连接OD,OE.
解:连接OD,OE.
则四边形ODEC是菱形.且面积是△ABC面积的$\frac{1}{2}$,
∴菱形ODEC的面积是:$\frac{\sqrt{3}}{2}$,
扇形DOE的圆心角是60°,则扇形DOE的面积是$\frac{60π×{1}^{2}}{360}$=$\frac{π}{6}$,
则阴影部分的面积是:$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
故答案是:$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
点评 本题主要考查了图形的面积的计算方法,不规则图形的面积可以转化为规则图形的面积的和或差的问题.

练习册系列答案
相关题目
10.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2-2b2,则( )
| A. | △ABC是直角三角形,且∠A为直角 | B. | △ABC是直角三角形,且∠B为直角 | ||
| C. | △ABC是直角三角形,且∠C为直角 | D. | △ABC不是直角三角形 |
7.下列各组单项式中,不是同类项的是( )
| A. | 3x2y与-2yx2 | B. | 2ab2与-ba2 | C. | $\frac{xy}{3}$与5xy | D. | 23a与32a |
4.正方形两条对角线之和为8cm,则它的面积为( )
| A. | 8 | B. | $4\sqrt{2}$ | C. | 4 | D. | 16 |
9.若点(-2,y1),(-1,y2),(1,y3)在反比例函数y=$\frac{4}{x}$的图象上,则下列说法正确的是( )
| A. | y1>y2>y3 | B. | y3>y2>y1 | C. | y3>y1>y2 | D. | y2>y1>y3 |
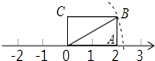 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是$±\sqrt{5}$.
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是$±\sqrt{5}$.