题目内容
 如图,已知C为BE上一点,点A、点D在BE的同侧,∠A=∠DCE,AC∥DE,BC=DE=6,AC=3.求BE的长度.
如图,已知C为BE上一点,点A、点D在BE的同侧,∠A=∠DCE,AC∥DE,BC=DE=6,AC=3.求BE的长度.考点:全等三角形的判定与性质
专题:几何图形问题
分析:由AC与DE平行,利用两直线平行同位角相等得到一对角相等,再由已知一对角相等,一对边相等,利用AAS得到三角形ABC与三角形DCE全等,利用全等三角形的性质得到AC=DE,再有BC+CE即可确定出BE的长.
解答:解:∵AC∥DE,
∴∠ACB=∠E,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS),
∴CE=AC=3,
则BE=BC+CE=6+3=9.
∴∠ACB=∠E,
在△ABC和△CDE中,
|
∴△ABC≌△CDE(AAS),
∴CE=AC=3,
则BE=BC+CE=6+3=9.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m. 如图,将△ABC绕着点O顺时针旋转90°后得到△A1B1C1,画出旋转后的△A1B1C1.
如图,将△ABC绕着点O顺时针旋转90°后得到△A1B1C1,画出旋转后的△A1B1C1.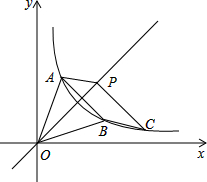 如图,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A的坐标为(1,3),A、B两点关于直线y=x对称,反比例函数y=
如图,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A的坐标为(1,3),A、B两点关于直线y=x对称,反比例函数y=