Question

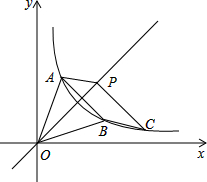如图，在平面直角坐标系中，△AOB的顶点O是坐标原点，点A的坐标为（1，3），A、B两点关于直线y=x对称，反比例函数y=

k

x

（x＞0）的图象经过点A，点P是直线y=x上一动点．
（1）点B的坐标为

 

；
（2）如图，若?ABCP的顶点C也在反比例函数y=

k

x

（x＞0）的图象上，求点C的坐标．

Answer 1

考点：反比例函数综合题

专题：综合题,待定系数法

分析：（1）由A与B关于y=x对称，根据A坐标确定出B坐标即可；
（2）将A坐标代入反比例解析式求出k的值，确定出反比例解析式，根据P在直线y=x上，设出P（m，m），与点A的横坐标比点B的横坐标小2，点A的纵坐标比点B的纵坐标大2，表示出C坐标，代入反比例解析式求出m的值，即可确定出C坐标．

解答：解：（1）∵A（1，3），A与B关于y=x对称，
∴B点的坐标为（3，1）；
（2）∵反比例函数y=

x

k

（x＞0）图象经过点A（1，3），
∴k=1×3=3，
∴反比例函数的解析式为y=

3

x

，
∵点P在直线y=x上，
∴设P（m，m）（m＞0），此时PC为平行四边形的边，
∵点A的横坐标比点B的横坐标小2，点A的纵坐标比点B的纵坐标大2，
∴点C的坐标为（m+2，m-2），
把C（m+2，m-2）代入反比例函数的解析式得：（m+2）（m-2）=3，
解得：m=±

7

，
∵m＞0，∴m=

7

＞0，
∴C（

7

+2，

7

-2）．
故答案为：（1）（3，1）

点评：此题考查了反比例函数综合题，涉及的知识有：对称的性质，待定系数法求反比例解析式，根据题意得出“点A的横坐标比点B的横坐标小2，点A的纵坐标比点B的纵坐标大2”是解本题的关键．