题目内容
二次函数y=x2+bx+c的图象经过点（4，3），（3，0）．
（1）求b、c的值；
（2）求该二次函数图象的顶点坐标和对称轴．
（1） ；（2）顶点坐标为（2，﹣1），对称轴为直线x=2
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式.
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴ ，
解得 ；
（2）∵该二次函数为y=x2﹣4x+3=（x...
导学与测试系列答案
新非凡教辅冲刺100分系列答案若函数y=mx²+(m+2)x+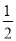
m+1的图象与x轴只有一个交点，那么m的值为( )
A. 0 B. 0或2 C. 2或－2 D. 0，2或－2
D
【解析】试题分析：当函数为一次函数时，则m=0；当函数为二次函数时，则，解得：m=±2.综上所述，m=0或2或－2. 对数轴上的点P进行如下操作：先把点P表示的数乘以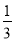
，再把所得数对应的点向右平移1个单位，得到点P的对应点P′，点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′，如图，若点A表示的数是﹣3，则点A′表示的数是__；若点B′表示的数是2，则点B表示的数是__．已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合，则点E表示的数是__．
0 3 1.5
【解析】试题分析：根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B表示的数为a，根据题意列出方程求解即可得到点B表示的数，设点E表示的数为b，根据题意列出方程计算即可得解．
试题解析：【解析】
点A′：﹣3×+1=﹣1+1=0．
设点B表示的数为a，则a+1=2，解得a=3．
设点E表示的数为b，则b+1=b，解得b=1.5．
故答... 如图，△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．由一个三角形变换到另一个三角形（ ）
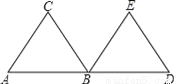
A. 仅能由平移得到
B. 仅能由旋转得到
C. 既能由平移得到，也能由旋转得到
D. 既不能由平移得到，也不能由旋转得到
C
【解析】【解析】
∵△ABC和△BDE是等边三角形，点A、B、D在一条直线上，并且AB=BD．
∴这三对全等三角形中的一个都是以其中另一个三角形绕点B旋转90°后得到或对折得到的．故选C． 如图，抛物线y=x2 +bx+c与x轴交于A（﹣1，0），B（3，0）两点．
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴以及顶点坐标；
（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．
（1）y=x2﹣2x﹣3；（2）抛物线的对称轴x=1，顶点坐标（1，﹣4）；（3）（，4）或（，4）或（1，﹣4）．
【解析】试题分析：（1）由于抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3，然后利用根与系数即可确定b、c的值．
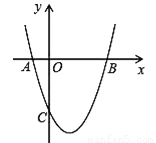
（2）根据S△PAB=8，求得P的纵坐标，把纵坐标代入抛物线的解析式即可求得... 已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1）、P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且﹣1＜x1＜x2，x3＜﹣1，则y1、y2、y3的大小关系为（ ）
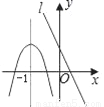
A. y1＜y2＜y3 B. y3＜y1＜y2 C. y3＜y2＜y1 D. y2＜y1＜y3
D
【解析】解析：对称轴为直线x=﹣1，且﹣1＜x1＜x2，当x＞﹣1时，y2＜y1，
又因为x3＜﹣1，由一次函数的图象可知，此时点P3（x3，y3）在二次函数图象上方，
所以y2＜y1＜y3．
故选：D． 关于二次函数y=x2﹣2x﹣3的图象，下列说法中错误的是（ ）
A. 当x＜2，y随x的增大而减小 B. 函数的对称轴是直线x=1
C. 函数的开口方向向上 D. 函数图象与y轴的交点坐标是（0，﹣3）
A
【解析】试题分析：∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴抛物线开口向上，对称轴为x=1，当x＜1时y随x的增大而减小，故B、C正确，A不正确，
令x=0可得y=﹣3，
∴抛物线与y轴的交点坐标为（0，﹣3），故D正确，
故选A． 已知：如图，在△ABC中有D、E两点，求证：BD＋DE＋EC＜AB＋AC．
见解析
【解析】试题分析：延长BD交AC于M点，延长CE交BD的延长线于点N．在△ABM中，AB+AM>BM，在△CNM中，NM+MC>NC，所以AB+AM+NM+MC>BM+NC，再由AM+MC=AC，BM=BN+NM可知AB+AC+NM>BN+NM+NC，故AB+AC>BN+NC，在△BNC中，BN+NC=BD+DN+NE+EC，在△DNE中，DN+NE>DE，由此即可得出结论．
... 已知函数y=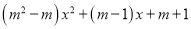
(1)若这个函数是一次函数，求m的值;
(2)若这个函数是二次函数，则m的值应怎样？
(1)、m=0；(2)、m≠0且m≠1.
【解析】试题分析：（1）由一次函数的定义求解；
（2）由二次函数的定义求解．
试题解析：（1）由一次函数的定义，得： ，解得m=0或m=1，又∵m﹣1≠0即m≠1；∴当m=0时，这个函数是一次函数；
（2）由二次函数的定义，得： ，解得且，∴当且时，这个函数是二次函数．