题目内容
7. 如图,在等腰梯形ABCD中,AB∥CD,AD=BC,将△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合;
如图,在等腰梯形ABCD中,AB∥CD,AD=BC,将△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合;(1)求证;四边形AMCD为菱形;
(2)求证:AC⊥BC;
(3)当AB=4时,求梯形ABCD的面积.
分析 (1)连接MC,根据对折前后的两个角完全重合,利用角的关系证明AD∥MC,然后证明出四边形AMCD是平行四边形,根据平行四边形的对边相等得到AM=CD,从而得到AM=MC,于是得到结论;
(2)由(1)证得AM=CM,点M是AB的中点,所以AM=MC=MB,从而得证;
(3)先证明△BCM是等边三角形,然后求出等边三角形BM边上的高,再利用梯形的面积公式列式计算即可.
解答 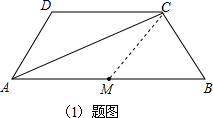 解:(1)如(1)题图,连接MC,
解:(1)如(1)题图,连接MC,
∵AB∥CD,
∴∠DCA=∠BAC,
∵∠DAC=∠BAC,∠DCA=∠MCA,
∴∠DAC=∠MCA,
∴AD∥MC,
∴四边形AMCD是平行四边形,
∴AM=CD,
∵△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合,
∴DC=MC,
∴AM=MC,
∴?AMCD是菱形;
(2)由(1)证得AM=CM
∵点M是AB的中点,
∴AM=BM,
∴AM=MC=BM,
∴∠ACB=90°,
∴AC⊥BC;
(3)如(2)题图,由(1)得四边形AMCD是平行四边形,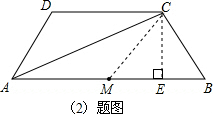
∴AD=MC,
∵AD=BC,
∴MC=BC,
∴△BCM是等边三角形,
∵AB=4,
∴BC=BM=$\frac{1}{2}$AB=2,
过点C作CE⊥MB,垂足为E,
则BE=$\frac{1}{2}$MB=1,
由勾股定理得,CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴梯形ABCD的面积=$\frac{1}{2}$(2+4)×$\sqrt{3}$=3$\sqrt{3}$.
点评 本题主要考查了等腰梯形的性质,平行四边形的判定与性质,等边三角形的判定与性质,勾股定理的应用,综合性较强,作出辅助线把梯形的问题转化为平行四边形与的问题是解题的关键.

 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简|a-b|+|a+b|的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简|a-b|+|a+b|的结果为( )| A. | 2a | B. | 2b | C. | -2a | D. | -2b |
 如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.
如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.

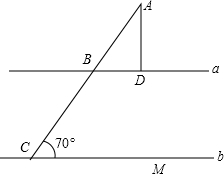 如图所示,已知a∥b,AD⊥直线a,求∠A的度数.
如图所示,已知a∥b,AD⊥直线a,求∠A的度数.