题目内容
8.在△ABC中,AB=9,AC=12,BC=18,D为AC上一点,AD=4,在AB上取一点E,得到△ADE,若这两个三角形相似,则它们的周长之比是1:3或4:9.分析 因为对应边不明确,所以分①AD与AC是对应边,②AD与AB是对应边,根据相似三角形对应边成比例列式求解即可.
解答 解:①AD与AC是对应边时,
∵AB=9,AC=12,AD=4,
∴相似比是$\frac{AD}{AC}=\frac{4}{12}$,
可得:它们的周长之比=1:3;
②AD与AB是对应边时,
∵AB=9,AC=12,AD=4,
∴相似比是$\frac{AD}{AB}=\frac{4}{9}$,
可得:它们的周长之比=4:9.
故答案为:1:3或4:9.
点评 本题考查了相似三角形对应边成比例的性质,根据对应边不明确,注意分情况讨论求解.

练习册系列答案
相关题目
 如图所示,点O在直线AE上,CO平分∠AOE,∠DOB是直角,则∠1的余角为∠DOE和∠BOC.
如图所示,点O在直线AE上,CO平分∠AOE,∠DOB是直角,则∠1的余角为∠DOE和∠BOC.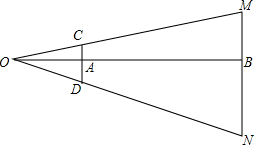 如图,小明家的窗口面对大楼,相距AB=80m,窗高CD=1.2m,小明从窗口后退2m,眼睛从点O处恰仔能看到楼顶M和楼底N,求大楼的高度.
如图,小明家的窗口面对大楼,相距AB=80m,窗高CD=1.2m,小明从窗口后退2m,眼睛从点O处恰仔能看到楼顶M和楼底N,求大楼的高度.