题目内容
3.我们定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,例如$|\begin{array}{l}{2}&{3}\\{4}&{5}\end{array}|$=2×5-3×4=10-12=-2,则不等式组1<$|\begin{array}{l}{1}&{x}\\{3}&{4}\end{array}|$<3的解集是$\frac{1}{3}$<x<1.分析 ,根据新定义列出不等式组,再分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:根据题意,得:$\left\{\begin{array}{l}{4-3x>1}&{①}\\{4-3x<3}&{②}\end{array}\right.$,
解不等式①,得:x<1,
解不等式②,得:x>$\frac{1}{3}$,
∴不等式组的解集为$\frac{1}{3}$<x<1,
故答案为:$\frac{1}{3}$<x<1.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
14. 如图,将△ABC绕点P顺时针旋转得到△A′B′C′,则点P的坐标是( )
如图,将△ABC绕点P顺时针旋转得到△A′B′C′,则点P的坐标是( )
 如图,将△ABC绕点P顺时针旋转得到△A′B′C′,则点P的坐标是( )
如图,将△ABC绕点P顺时针旋转得到△A′B′C′,则点P的坐标是( )| A. | (1,1) | B. | (1,5) | C. | (1,2) | D. | (1,4) |
8.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三边形,正四边形,正六边形,则另外一个为( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
15.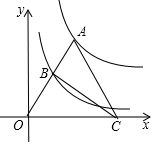 如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )
如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )
 如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )
如图,点A为函数y=$\frac{16}{x}$(x>0)图象上一点,连接OA,交函数y=$\frac{4}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
12.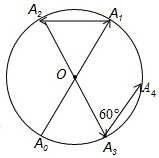 如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
 如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 0 |
13. 如图,AB∥CD,∠1=50°,∠2的度数是( )
如图,AB∥CD,∠1=50°,∠2的度数是( )
 如图,AB∥CD,∠1=50°,∠2的度数是( )
如图,AB∥CD,∠1=50°,∠2的度数是( )| A. | 50° | B. | 100° | C. | 130° | D. | 140° |