题目内容
12.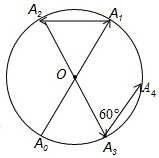 如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 0 |
分析 根据题意求得A0A1=4,A0A2=2$\sqrt{3}$,A0A3=2,A0A4=2$\sqrt{3}$,A0A5=2,A0A6=0,A0A7=4,…于是得到A2017与A1重合,即可得到结论.
解答  解:如图,∵⊙O的半径=2,
解:如图,∵⊙O的半径=2,
由题意得,A0A1=4,A0A2=2$\sqrt{3}$,A0A3=2,A0A4=2$\sqrt{3}$,A0A5=2,A0A6=0,A0A7=4,…
∵2017÷6=336…1,
∴按此规律运动到点A2017处,A2017与A1重合,
∴A0A2017=2R=4.
故选A.
点评 本题考查了图形的变化类,等边三角形的性质,解直角三角形,正确的作出图形是解题的关键.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | 3x-2x=1 | B. | (-a3)2=-a6 | C. | x6÷x2=x3 | D. | x3•x2=x5 |
7.两条直线y=k1x+b1和y=k2x+b2相交于点A(3,4),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ |
1.下列调查中,适宜采用全面调查方式的是( )
| A. | 了解长江中鱼的种类 | B. | 对“最强大脑”节目收视率的调查 | ||
| C. | 调查我国网名对某事件的看法 | D. | 对某班50名同学体重情况的调查 |
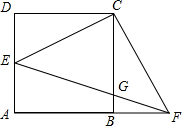 如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.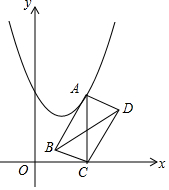 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为2.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为2.