题目内容
1.2014年6月,某中学以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图①和图②提供的信息,解答下列问题:(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图①)补充完整;
(3)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书箱的学生人数.

分析 (1)用文学的人数除以所占的百分比计算即可得解;
(2)根据所占的百分比求出艺术和其它的人数,然后补全折线图即可;
(3)用总人数乘以科普所占的百分比,计算即可得解.
解答  解:(1)90÷30%=300(名),
解:(1)90÷30%=300(名),
故一共调查了300名学生;
(2)艺术的人数:300×20%=60名,
其它的人数:300×10%=30名;
折线图补充如右图;
(3)1800×$\frac{80}{300}$=480(名).
答:1800名学生中估计最喜爱科普类书籍的学生为480名.
点评 本题考查的是折线统计图和扇形统计图的综合运用,折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况,扇形统计图中每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.也考查了利用样本估计总体.

练习册系列答案
相关题目
11.已知a、b、c为非零实数,且满足$\frac{b+c}{a}=\frac{a+b}{c}=\frac{a+c}{b}=k$,则一次函数y=kx+k+1的图象一定经过( )
| A. | 第一、二、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 第二象限 |
12.下列选项中,可以用来证明命题“若|a-1|>1,则a>2”是假命题的反例是( )
| A. | a=2 | B. | a=1 | C. | a=0 | D. | a=-1 |
16.某班的9名学生的体重分别是(单位:千克):70,67,65,63,61,59,59,57,59,这组数据的众数和中位数是( )
| A. | 59,61 | B. | 59,63 | C. | 59,65 | D. | 57,61 |
10.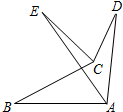 如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )
如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )
 如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )
如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )| A. | ∠AEC=∠ABC-2∠ADC | B. | ∠AEC=$\frac{∠ABC-∠ADC}{2}$ | ||
| C. | ∠AEC=$\frac{1}{2}$∠ABC-∠ADC | D. | ∠AEC=$\frac{∠ABC-∠ADC}{3}$ |