题目内容
6.某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若超市购进x(x>0)件甲种玩具需要花费y元,求y与x的函数关系式;
(3)超市打算购买x件(x>20)玩具,在(2)的条件下,从甲、乙两种玩具中选购其中一种,问:当x满足什么条件时超市购进甲种玩具比购进乙种玩具更省钱?
分析 (1)设每件甲种玩具的进价是x元,每件乙种玩具的进价是y元,根据“5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元”列出方程组解决问题;
(2)分情况:不大于20件;大于20件;分别列出函数关系式即可;
(3)设购进玩具x件(x>20),分别表示出甲种和乙种玩具消费,建立不等式解决问题.
解答 解:(1)设每件甲种玩具的进价是x元,每件乙种玩具的进价是y元,
由题意得:$\left\{\begin{array}{l}{5x+3y=231}\\{2x+3y=141}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=30}\\{y=27}\end{array}\right.$.
答:件甲种玩具的进价是30元,每件乙种玩具的进价是27元;
(2)当0<x≤20时,y=30x;
当x>20时,y=20×30+(x-20)×30×0.7=21x+180;
(3)设购进玩具x件(x>20),则乙种玩具消费27x元,甲种玩具消费(21x+180)元,
当27x>21x+180,则x>30,
所以当购进玩具超过30件,选择购甲种玩具省钱.
点评 此题考查二元一次方程组,一次函数,一元一次不等式的运用,解决本题的关键是理解题意,正确列式解决问题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
16. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )
 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则图中相等的线段共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
 如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:
如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:
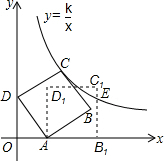 如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )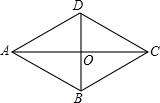 如图,已知菱形ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,则AB=5.
如图,已知菱形ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,则AB=5.