题目内容
6.解方程:(1)$\frac{x}{x-1}$=1+$\frac{2}{x}$.
(2)$\frac{2}{x+1}$-$\frac{3}{1-x}$=$\frac{6}{{x}^{2}-1}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x2=x2-x+2x-2,
解得:x=2,
经检验x=2是分式方程的解;
(2)去分母得:2x-2+3x+3=6,
解得:x=1,
经检验x=1是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
1.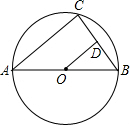 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,如果AC:BC=4:3,AB=10cm,那么BD的长为( )
如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,如果AC:BC=4:3,AB=10cm,那么BD的长为( )
 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,如果AC:BC=4:3,AB=10cm,那么BD的长为( )
如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于D,如果AC:BC=4:3,AB=10cm,那么BD的长为( )| A. | 3cm | B. | $\frac{3}{2}$cm | C. | 6cm | D. | 12cm |
11. 已知有理数a、b在数轴上对应点的位置如图所示,且|a|>|b|,则|a|-|a+b|-|b-a|的值为( )
已知有理数a、b在数轴上对应点的位置如图所示,且|a|>|b|,则|a|-|a+b|-|b-a|的值为( )
 已知有理数a、b在数轴上对应点的位置如图所示,且|a|>|b|,则|a|-|a+b|-|b-a|的值为( )
已知有理数a、b在数轴上对应点的位置如图所示,且|a|>|b|,则|a|-|a+b|-|b-a|的值为( )| A. | 2b+a | B. | 2b-a | C. | a | D. | b |
18.下列说法正确的是( )
| A. | 正数和负数统称为有理数 | B. | 任何正数一定大于它的倒数 | ||
| C. | -a一定是负数 | D. | 互为相反数的两个数之和为零 |
 如图,已知OM,ON分别是∠AOB,∠BOC的平分线,射线OP在∠AOC的内部,若要使∠AOP与∠MON相等,则OP应满足什么条件?为什么?
如图,已知OM,ON分别是∠AOB,∠BOC的平分线,射线OP在∠AOC的内部,若要使∠AOP与∠MON相等,则OP应满足什么条件?为什么?