题目内容
设a,b是方程x2+x-9=0的两个实数根,则a2+2a+b的值为 .
考点:根与系数的关系,一元二次方程的解
专题:
分析:由于a2+2a+b=(a2+a)+(a+b),故根据方程的解的意义,求得(a2+a)的值,由根与系数的关系得到(a+b)的值,即可求解.
解答:解:∵a是方程x2+x-9=0的根,
∴a2+a=9;
由根与系数的关系得:a+b=-1,
∴a2+2a+b=(a2+a)+(a+b)=9+(-1)=8.
故答案为:8.
∴a2+a=9;
由根与系数的关系得:a+b=-1,
∴a2+2a+b=(a2+a)+(a+b)=9+(-1)=8.
故答案为:8.
点评:本题考查了一元二次方程的解的定义及根与系数的关系,要正确解答本题还要能对代数式进行恒等变形.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列说法正确的个数有( )
①|a|一定是正数;②-a一定是负数;③-(-a)一定是正数;④
一定是分数.
①|a|一定是正数;②-a一定是负数;③-(-a)一定是正数;④
| a |
| 7 |
| A、0个 | B、1个 | C、2个 | D、3个 |
把抛物线y=x2+1向右平移3个单位,再向下平移2个单位,得到抛物线( )
| A、y=(x+3)2-1 |
| B、y=(x+3)2+3 |
| C、y=(x-3)2-1 |
| D、y=(x-3)2+3 |
若方程4x-1=3x+1和2m+x=1的解相同,则m的值为( )
| A、-3 | ||
| B、1 | ||
C、-
| ||
D、
|
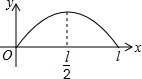 点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点间的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )


 如图,OE平分∠AOC,OF平分∠BOC,∠AOE=25°,∠COF=40°,∠AOB=
如图,OE平分∠AOC,OF平分∠BOC,∠AOE=25°,∠COF=40°,∠AOB=