题目内容
把抛物线y=x2+1向右平移3个单位，再向下平移2个单位，得到抛物线（ ）
| A、y=（x+3）2-1 |
| B、y=（x+3）2+3 |
| C、y=（x-3）2-1 |
| D、y=（x-3）2+3 |
考点：二次函数图象与几何变换
专题：
分析：易得原抛物线的顶点及平移后抛物线的顶点，根据平移不改变抛物线的二次项系数可得新的抛物线解析式．
解答：解：由题意得原抛物线的顶点为（0，1），
∴平移后抛物线的顶点为（3，-1），
∴新抛物线解析式为y=（x-3）2-1，
故选：C．
∴平移后抛物线的顶点为（3，-1），
∴新抛物线解析式为y=（x-3）2-1，
故选：C．
点评：考查二次函数的几何变换；用到的知识点为：二次函数的平移不改变二次项的系数；得多新抛物线的顶点是解决本题的突破点．
练习册系列答案
阅读快车系列答案
相关题目
-5的相反数是（ ）
A、
| ||
| B、-5 | ||
C、-
| ||
| D、5 |
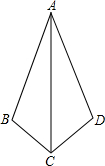如图，∠BAC=∠DAC，∠B=∠D．求证：AB=AD．