题目内容
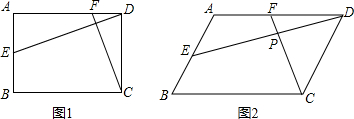
四边形ABCD中,点E是AB的中点,F是AD边上的动点.连结DE、CF.
(1)若四边形ABCD是矩形,AD=12,CD=10,如图(1).
①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度.
(2)如图(2),若四边形ABCD是平行四边形,DE与CF相交于点P.探究:当∠B与∠EPC满足什么关系时,
=
成立?并证明你的结论.
(1)若四边形ABCD是矩形,AD=12,CD=10,如图(1).
①请直接写出AE的长度;
②当DE⊥CF时,试求出CF长度.
(2)如图(2),若四边形ABCD是平行四边形,DE与CF相交于点P.探究:当∠B与∠EPC满足什么关系时,
| DE |
| CF |
| AD |
| CD |

考点:四边形综合题
专题:
分析:(1)①根据矩形的性质和中点的定义就可以得出AE的值;
②根据勾股定理就可以求出ED的值,再由△CFD∽△DEA,由相似三角形的性质就可以求出结论;
(2)当∠B+∠EPC=180°时,
=
成立,证△DFP∽△DEA,得出
=
,证△CPD∽△CDF,得出
=
,即可得出答案.
②根据勾股定理就可以求出ED的值,再由△CFD∽△DEA,由相似三角形的性质就可以求出结论;
(2)当∠B+∠EPC=180°时,
| DE |
| CF |
| AD |
| CD |
| DE |
| AD |
| DF |
| DP |
| DF |
| DP |
| CF |
| CD |
解答:解:(1)①∵四边形ABCD是矩形,
∴AD=BC,AB=CD,∠A=∠ADC=90°.
∵AD=12,CD=10,
∴BC=12,AB=10.
∵点E是AB的中点,
∴AE=
AB=5.
②∵DE⊥CF,
∴∠DPC=∠DPF=90°,
∴∠DFC+∠DCF=90°,∠DFC+∠FDP=90°,
∴∠DCF=∠FDP.
∵∠A=∠ADC,
∴△CFD∽△DEA,
∴
=
.
在Rt△AED中,由勾股定理,得
ED=13.
∴
=
,
∴CF=
.
答:CF的长度为
;
(2)当∠B+∠EPC=180°时,
=
成立.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠B+∠A=180°,
∵∠B+∠EPC=180°,
∴∠A=∠EPC=∠FPD,
∵∠FDP=∠EDA,
∴△DFP∽△DEA,
∴
=
,
∵∠B=∠ADC,∠B+∠EPC=180°,∠EPC+∠DPC=180°,
∴∠CPD=∠CDF,
∵∠PCD=∠DCF,
∴△CPD∽△CDF,
∴
=
,
∴
=
∴
=
,
即当∠B+∠EPC=180°时,
=
成立.
∴AD=BC,AB=CD,∠A=∠ADC=90°.

∵AD=12,CD=10,
∴BC=12,AB=10.
∵点E是AB的中点,
∴AE=
| 1 |
| 2 |
②∵DE⊥CF,
∴∠DPC=∠DPF=90°,
∴∠DFC+∠DCF=90°,∠DFC+∠FDP=90°,
∴∠DCF=∠FDP.
∵∠A=∠ADC,
∴△CFD∽△DEA,
∴
| CD |
| AD |
| CF |
| ED |
在Rt△AED中,由勾股定理,得
ED=13.
∴
| 10 |
| 12 |
| CF |
| 13 |
∴CF=
| 65 |
| 6 |
答:CF的长度为
| 65 |
| 6 |
(2)当∠B+∠EPC=180°时,
| DE |
| CF |
| AD |
| CD |
证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠B+∠A=180°,
∵∠B+∠EPC=180°,
∴∠A=∠EPC=∠FPD,
∵∠FDP=∠EDA,
∴△DFP∽△DEA,
∴
| DE |
| AD |
| DF |
| DP |
∵∠B=∠ADC,∠B+∠EPC=180°,∠EPC+∠DPC=180°,
∴∠CPD=∠CDF,
∵∠PCD=∠DCF,
∴△CPD∽△CDF,
∴
| DF |
| DP |
| CF |
| CD |
∴
| DE |
| AD |
| CF |
| CD |
∴
| DE |
| CF |
| AD |
| CD |
即当∠B+∠EPC=180°时,
| DE |
| CF |
| AD |
| CD |
点评:本题考查了矩形性质和判定,勾股定理,平行四边形的性质和判定,全等三角形的性质和判定,相似三角形的性质和判定的应用,主要考查学生综合运用性质和定理进行推理的能力.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
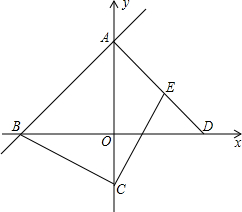 已知,如图:直线AB:y=x+8与x轴、y轴分别相交于点B、A,过点A作直线AB的垂线交x轴于点D.
已知,如图:直线AB:y=x+8与x轴、y轴分别相交于点B、A,过点A作直线AB的垂线交x轴于点D. 如图,平行四边形AOBC中,对角线AB,OC相交于点E,双曲线y=
如图,平行四边形AOBC中,对角线AB,OC相交于点E,双曲线y= 如图,在?ABCD中,E在DC上,若DE:EC=1:2,则EF:BF=
如图,在?ABCD中,E在DC上,若DE:EC=1:2,则EF:BF=