题目内容
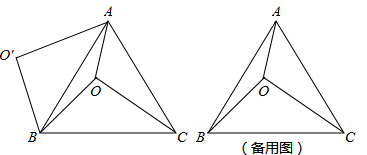
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO绕点B逆时针旋转60°得到线段BO′.
(1)求点O与O′的距离;
(2)证明:∠AOB=150°;
(3)求四边形AOBO′的面积.
(4)直接写出△AOC与△AOB的面积和为 .
(1)求点O与O′的距离;
(2)证明:∠AOB=150°;
(3)求四边形AOBO′的面积.
(4)直接写出△AOC与△AOB的面积和为

考点:旋转的性质,全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)证明△BO′A≌△BOC,即可证明△OBO′是等边三角形,从而求解;
(2)利用勾股定理的逆定理即可证得△AOO′是直角三角形,即可求解;
(3)根据S四边形AOBO'=S△AOO'+S△OBO'即可求解;
(4)将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点,根据S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″求解.
(2)利用勾股定理的逆定理即可证得△AOO′是直角三角形,即可求解;
(3)根据S四边形AOBO'=S△AOO'+S△OBO'即可求解;
(4)将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点,根据S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″求解.
解答: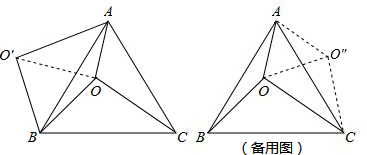 解:(1)∵等边△ABC,
解:(1)∵等边△ABC,
∴AB=CB,∠ABC=60°.
∵线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,
∴BO=BO′,∠O′AO=60°.
∴∠O′BA=60°-∠ABO=∠OBA.
在△BO'A和△BOC中,
,
∴△BO′A≌△BOC(SAS).
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到.
连接OO′,
∵BO=BO′,∠O′AO=60°,
∴△OBO′是等边三角形.
∴OO′=OB=4.
(2)∵△AOO′中,
三边长为O′A=OC=5,OO′=OB=4,OA=3,是一组勾股数,
∴△AOO′是直角三角形.
∴∠AOB=∠AOO′+∠O′OB=90°+600=150°.
(3)S四边形AOBO'=S△AOO'+S△OBO'=
×3×4+
×4×2
=6+4
.
(4)如图,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形.
则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=
×3×4+
×3×
=6+
.
 解:(1)∵等边△ABC,
解:(1)∵等边△ABC,∴AB=CB,∠ABC=60°.
∵线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,
∴BO=BO′,∠O′AO=60°.
∴∠O′BA=60°-∠ABO=∠OBA.
在△BO'A和△BOC中,
|
∴△BO′A≌△BOC(SAS).
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到.
连接OO′,
∵BO=BO′,∠O′AO=60°,
∴△OBO′是等边三角形.
∴OO′=OB=4.
(2)∵△AOO′中,
三边长为O′A=OC=5,OO′=OB=4,OA=3,是一组勾股数,
∴△AOO′是直角三角形.
∴∠AOB=∠AOO′+∠O′OB=90°+600=150°.
(3)S四边形AOBO'=S△AOO'+S△OBO'=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(4)如图,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形.
则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
9
| ||
| 4 |
点评:本题考查了图形的旋转,正确作出辅助线是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个三角形的两边长为3和8,第三边的边长是x(x-9)-13(x-9)=0的根,则这个三角形的周长是( )
| A、20 | B、20或24 |
| C、9和13 | D、24 |
下列说法中,错误的是( )
| A、四个角都相等的四边形是矩形 |
| B、每组邻边都相等的四边形是菱形 |
| C、对角线互相垂直的平行四边形是正方形 |
| D、对角线互相平分的四边形是平行四边形 |
函数y=2x-5中,若y不小于3,则x的范围是( )
| A、不小于4 | B、不大于4 |
| C、大于4 | D、不小于3 |
某商店将某种服装先按成本提高60%标价,再以8折优惠卖出,结果每件服装仍可获利28元,则这种服装每件的成本价是( )
| A、240元 | B、100元 |
| C、120元 | D、95元 |
 如图,已知直线AB∥CD,∠ABE=60°,∠CDE=20°,求∠BED的度数.
如图,已知直线AB∥CD,∠ABE=60°,∠CDE=20°,求∠BED的度数.