题目内容
如图，平行四边形AOBC中，对角线AB，OC相交于点E，双曲线y=| k |
| x |
（1）求证：AM=2EN；
（2）若平行四边形AOBC的面积为24，求k的值．
考点：反比例函数综合题
专题：
分析：（1）首先根据四边形AOBC是平行四边形，得到AE=EB，再根据题干条件AM⊥OB，EN⊥OB，得到AM∥EN，于是得到
=
=
，结论即可得出；
（2）根据题意得到BN=MN，又知AM×OM=EN×ON=k，AM=2EM，即可得到ON=2OM，得到OM=MN=BN，最后根据平行四边形AOBC的面积为24，得到k的值．
| EN |
| AM |
| BE |
| AB |
| 1 |
| 2 |
（2）根据题意得到BN=MN，又知AM×OM=EN×ON=k，AM=2EM，即可得到ON=2OM，得到OM=MN=BN，最后根据平行四边形AOBC的面积为24，得到k的值．
解答：（1）证明：在平行四边形AOBC中，AE=EB，
∵AM⊥OB，EN⊥OB，
∴AM∥EN，
∴
=
=
，
∴AM=2EN；
（2）解：∵
=
，
∴BN=MN，
∵AM×OM=EN×ON=k，AM=2EN，
∴ON=2OM，
∴OM=MN=NB，
∵OB×AM=24，
∴3OM×AM=24，
∴k=OM×AM=8．
∵AM⊥OB，EN⊥OB，
∴AM∥EN，
∴
| EN |
| AM |
| BE |
| AB |
| 1 |
| 2 |
∴AM=2EN；
（2）解：∵
| BN |
| MN |
| BE |
| AE |
∴BN=MN，
∵AM×OM=EN×ON=k，AM=2EN，
∴ON=2OM，
∴OM=MN=NB，
∵OB×AM=24，
∴3OM×AM=24，
∴k=OM×AM=8．
点评：本题主要考查反比例函数的综合题，解答本题的关键是熟练掌握反比例函数的性质以及系数k的意义，此题难度不大，是一道不错的试题．
练习册系列答案
相关题目
如图，已知直线AB∥CD，∠ABE=60°，∠CDE=20°，求∠BED的度数．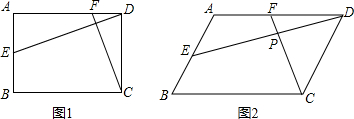
已知：如图，在平面直角坐标系xOy中，直线AB分别与x、y轴交于点B、A，与函数
如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=8cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么AD的长是