题目内容
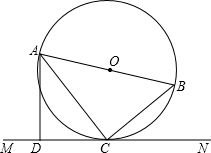 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.(1)求证:MN是⊙O的切线;
(2)若CD=6,cos∠ACD=
| 3 |
| 5 |
考点:切线的判定
专题:
分析:(1)连接OC,推出AD∥OC,推出OC⊥MN,根据切线的判定推出即可;
(2)求出AD、AB长,证△ADC∽△ACB,得出比例式,代入求出AB长即可.
(2)求出AD、AB长,证△ADC∽△ACB,得出比例式,代入求出AB长即可.
解答: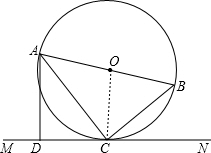 解:(1)直线MN与⊙0的位置关系是相切,
解:(1)直线MN与⊙0的位置关系是相切,
理由是:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠CAB=∠DAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥MN,
∴OC⊥MN,
∵OC为半径,
∴MN是⊙O切线;
(2)∵CD=6,cos∠ACD=
=
,
∴AC═10,由勾股定理得:AD=8,
∵AB是⊙O直径,AD⊥MN,
∴∠ACB=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
=
,
∴
=
,
∴AB=12.5,
∴⊙O半径是
×12.5=6.25.
 解:(1)直线MN与⊙0的位置关系是相切,
解:(1)直线MN与⊙0的位置关系是相切,理由是:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠CAB=∠DAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥MN,
∴OC⊥MN,
∵OC为半径,
∴MN是⊙O切线;
(2)∵CD=6,cos∠ACD=
| DC |
| AC |
| 3 |
| 5 |
∴AC═10,由勾股定理得:AD=8,
∵AB是⊙O直径,AD⊥MN,
∴∠ACB=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴
| AD |
| AC |
| AC |
| AB |
∴
| 8 |
| 10 |
| 10 |
| AB |
∴AB=12.5,
∴⊙O半径是
| 1 |
| 2 |
点评:本题考查了切线的判定,等腰三角形的判定和性质,平行线性质,相似三角形的性质和判定的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
相关题目
下列各组数可能构成一个三角形的是( )
| A、2,2,4 |
| B、3,5,9 |
| C、4,7,8 |
| D、5,5,11 |
 在菱形ABCD中,下列结论一定正确的是( )
在菱形ABCD中,下列结论一定正确的是( )| A、AD=BD |
| B、菱形ABCD的面积是AC和BD的积 |
| C、∠DAC=∠BAC |
| D、∠ACB=30° |
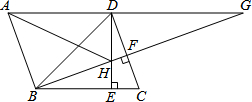 如图,?ABCD中,∠DBC=45°,高线DE、BF交于点H,BF、AD的延长线交于点G;联结AH.
如图,?ABCD中,∠DBC=45°,高线DE、BF交于点H,BF、AD的延长线交于点G;联结AH.

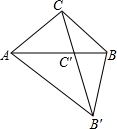 如图,在三角形ABC中,∠A=40°,△ABC绕点A旋转后点C落在边AB上的点C′,点B落到点B′,如果点C、C′、B′在同一直线上,那么∠ABC的度数是
如图,在三角形ABC中,∠A=40°,△ABC绕点A旋转后点C落在边AB上的点C′,点B落到点B′,如果点C、C′、B′在同一直线上,那么∠ABC的度数是