题目内容
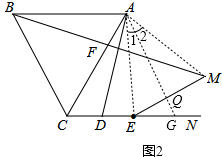
已知等边三角形ABC,F为AC上一点,以AC为一边∠ACN=60°,D、E为CN上一点,且CD=AF,
(1)求证:BF=AD;
(2)若CD=DE,延长BF到M,使FM=BF,连接ME,请你判断直线BC与直线ME的位置关系,并证明你的结论.

(1)求证:BF=AD;
(2)若CD=DE,延长BF到M,使FM=BF,连接ME,请你判断直线BC与直线ME的位置关系,并证明你的结论.

考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)运用等边三角形的性质直接由SAS得出△ABF≌△CAD就可以得出BF=AD;
(2)连接AE,AM,作AG∥BC交EM于Q,CN与G,通过证明△AFM≌△EDA就可以得出AM=EA,∠MAF=∠AED,再由平行四边形的性质就可以∠ABC=∠AGC=60°,就有∠CAG=60°,∠FAM=60°+∠2,∠AED=60°+∠1,就可以得出∠1=∠2,由等腰三角形的性质及可以得出AG⊥ME,得出BC⊥ME.
(2)连接AE,AM,作AG∥BC交EM于Q,CN与G,通过证明△AFM≌△EDA就可以得出AM=EA,∠MAF=∠AED,再由平行四边形的性质就可以∠ABC=∠AGC=60°,就有∠CAG=60°,∠FAM=60°+∠2,∠AED=60°+∠1,就可以得出∠1=∠2,由等腰三角形的性质及可以得出AG⊥ME,得出BC⊥ME.
解答:解:(1)∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵∠ACN=60°,
∴∠BAC=∠ACN.
在△ABF和△CAD中,
,
∴△ABF≌△CAD(SAS),
∴BF=AD;
(2)BC⊥ME,
理由:连接AE,AM,作AG∥BC交EM于Q,CN与G,
∵△ABC为等边三角形,
∴∠BAC=∠ABC=60°,AB=AC,
∵∠ACN=60°,
∴∠BAC=∠ACN.
∴AB∥CN.
∴四边形ABCG是平行四边形,
∴∠AGC=∠ABC=60°.
∴∠CAG=60°.
∵MF=BF,
∴MF=AD.
∵△ABF≌△CAD,
∴∠ABF=∠CAD.
∴∠ABF+∠BAC=∠CAD+∠ACN
∵∠AFM=∠ABF+∠BAC,∠ADE=∠CAD+∠ACN,
∴∠AFM=∠ADE.
∵CD=DE,
∴AF=DE.
在△AFM和△EDA中
,
∴△AFM≌△EDA(SAS),
∴AM=EA,∠MAF=∠AED.
∵∠MAF=∠CAG+∠2=60°+∠2,∠AED=∠AGC+∠1=60°+∠1,
∴∠2=∠1.
∴AG⊥ME,
∴BC⊥ME.
∴∠BAC=60°,AB=AC,
∵∠ACN=60°,
∴∠BAC=∠ACN.
在△ABF和△CAD中,
|
∴△ABF≌△CAD(SAS),
∴BF=AD;
(2)BC⊥ME,
理由:连接AE,AM,作AG∥BC交EM于Q,CN与G,
∵△ABC为等边三角形,
∴∠BAC=∠ABC=60°,AB=AC,
∵∠ACN=60°,
∴∠BAC=∠ACN.
∴AB∥CN.
∴四边形ABCG是平行四边形,
∴∠AGC=∠ABC=60°.
∴∠CAG=60°.
∵MF=BF,
∴MF=AD.
∵△ABF≌△CAD,
∴∠ABF=∠CAD.
∴∠ABF+∠BAC=∠CAD+∠ACN
∵∠AFM=∠ABF+∠BAC,∠ADE=∠CAD+∠ACN,
∴∠AFM=∠ADE.
∵CD=DE,
∴AF=DE.
在△AFM和△EDA中
|
∴△AFM≌△EDA(SAS),
∴AM=EA,∠MAF=∠AED.
∵∠MAF=∠CAG+∠2=60°+∠2,∠AED=∠AGC+∠1=60°+∠1,
∴∠2=∠1.
∴AG⊥ME,
∴BC⊥ME.

点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,等腰三角形的性质的运用,平行四边形的判定及性质的运用,三角形的外角与内角的关系的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
-
的相反数是( )
| 1 |
| 7 |
| A、-7 | ||
| B、7 | ||
C、
| ||
D、-
|
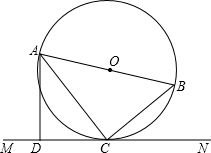 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.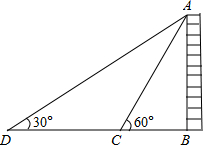 如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少?
如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为多少? 若一次函数y=kx+b(k,b为常数,且k=0)的图象如图,根据图象信息,则关于x的不等式kx+b>3的解为
若一次函数y=kx+b(k,b为常数,且k=0)的图象如图,根据图象信息,则关于x的不等式kx+b>3的解为