题目内容
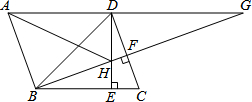 如图,?ABCD中,∠DBC=45°,高线DE、BF交于点H,BF、AD的延长线交于点G;联结AH.
如图,?ABCD中,∠DBC=45°,高线DE、BF交于点H,BF、AD的延长线交于点G;联结AH.(1)求证:BH=AB;
(2)求证:AH•BG=AG•BD.
考点:平行四边形的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)根据已知利用AAS判定△BEH≌△DEC,从而得到BH=DC,由平行四边形的性质得DC=AB,则可以得到AB=BH;
(2)根据两组角对应相等的两个三角形相似得到△GDB∽△GHA,相似三角形的对应边成比例,所以AH•BG=AG•BD.
(2)根据两组角对应相等的两个三角形相似得到△GDB∽△GHA,相似三角形的对应边成比例,所以AH•BG=AG•BD.
解答:(1)证明:
∵DE、BF是高,
∴∠BED=∠DEC=∠BFC=90°,
∴∠EBH+∠C=90°,∠EDC+∠C=90°∠DBC+∠EDB=90°
∴∠EDC=∠EBH,
∵∠DBC=45°,
∴∠EDB=∠DBC=45°,
∴BE=DE,
在△BEH与△DEC中,
,
∴△BEH≌△DECASA),
∴BH=DC,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴BH=AB;
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠ADB=∠DBC=45°,
∴AB∥DC,
∴∠ABH=∠BFC=90°,
∵AB=BH,
∴∠BHA=∠BAH=45°,
∵∠GDB+∠ADB=180°,∠GHA+∠AHB=180°
∴∠GHA=∠GDB,
又∵∠G=∠G,
∴△GHA∽△GDB,
∴
=
,
即AH•BG=AG•BD.
∵DE、BF是高,
∴∠BED=∠DEC=∠BFC=90°,
∴∠EBH+∠C=90°,∠EDC+∠C=90°∠DBC+∠EDB=90°
∴∠EDC=∠EBH,
∵∠DBC=45°,
∴∠EDB=∠DBC=45°,
∴BE=DE,
在△BEH与△DEC中,
|
∴△BEH≌△DECASA),
∴BH=DC,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴BH=AB;
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠ADB=∠DBC=45°,
∴AB∥DC,
∴∠ABH=∠BFC=90°,
∵AB=BH,
∴∠BHA=∠BAH=45°,
∵∠GDB+∠ADB=180°,∠GHA+∠AHB=180°
∴∠GHA=∠GDB,
又∵∠G=∠G,
∴△GHA∽△GDB,
∴
| GA |
| GB |
| AH |
| BD |
即AH•BG=AG•BD.
点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及平行四边形的性质.此题难度适中,注意掌握数形结合思想的应用是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(3-
|
A、±(3-
| ||
B、3±
| ||
C、3-
| ||
D、
|
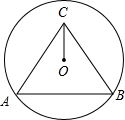 如图,圆O过点B、C,圆心O在正△ABC的内部,AB=2
如图,圆O过点B、C,圆心O在正△ABC的内部,AB=2| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|

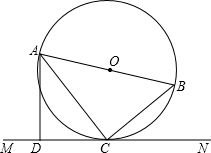 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.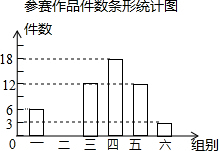 某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答:
某校举办“科技创新”作品评比,作品上交时限为3月1日至30日,组委会把同学们交来的作品按顺序每5天组成一组,共分成六组,现对每一组的件数进行统计,绘制成如图所示的不完全统计图.已知第二组与第四组的件数比为1:2.请你回答: