题目内容
19.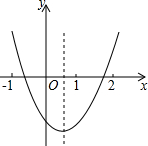 如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0,
如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0,③b2-4ac>0,④ac>0,其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 令x=1代入可判断①;由对称轴表达式的范围可判断②;由图象与x轴有两个交点可判断③;由开口方向及与x轴的交点可分别得出a、c的符号,可判断④.
解答 解:由图象可知当x=1时,y<0,
∴a+b+c<0,
故①不正确;
由图象可知0<-$\frac{b}{2a}$<1,
∴$\frac{b}{2a}$>-1,
又∵开口向上,
∴a>0,
∴b>-2a,
∴2a+b>0,
故②正确;
由图象可知二次函数与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴△>0,即b2-4ac>0,
故③正确;
由图象可知抛物线开口向上,与y轴的交点在x轴的下方,
∴a>0,c<0,
∴ac<0,
故④不正确;
综上可知正确的为②③,
故选B.
点评 本题考查了二次函数的图象与系数的关系,以及二次函数的图象和性质,掌握二次函数的开口方向、对称轴、与x轴的交点等知识是解题的关键.

练习册系列答案
相关题目
4.学习完一次函数后,小荣遇到过这样的一个新颖的函数:y=|x-1|,小荣根据学校函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小荣的探究过程,请补充完成:
(1)列表:下表是y与x的几组对应值,请补充完整.
(2)描点连线:在平面直角坐标系xOy中,请描出以上表中各对对应值为坐标的点,画出该函数的图象;
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合函数的图象,写出该函数的其他性质(一条即可):当x<0时,y随x的增大而减小.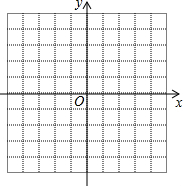
(1)列表:下表是y与x的几组对应值,请补充完整.
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 4 | 3 | 2 | 1 | 0 | 1 | 2 | … |
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合函数的图象,写出该函数的其他性质(一条即可):当x<0时,y随x的增大而减小.

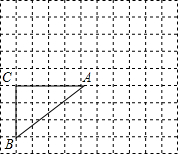 下列网格图中,每个小正方形边长均为1个单位,在Rt△ABC中,AC=4,BC=3,∠C=90°.若点B的坐标为(-3,-3),试在图中画出平面直角坐标系,根据所建立的坐标系,在给出的网格中作出与△ABC位似的△A1B1C1,使得位似中心为原点,△A1B1C1与△ABC的相似比是2,并写出A1、B1、C1点的坐标.
下列网格图中,每个小正方形边长均为1个单位,在Rt△ABC中,AC=4,BC=3,∠C=90°.若点B的坐标为(-3,-3),试在图中画出平面直角坐标系,根据所建立的坐标系,在给出的网格中作出与△ABC位似的△A1B1C1,使得位似中心为原点,△A1B1C1与△ABC的相似比是2,并写出A1、B1、C1点的坐标. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.