题目内容
 (1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;
(1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;(2)如图,过BC上一点P作BC的垂线交抛物线于点M、N,若PM•PN=4,求P点坐标.
考点:抛物线与x轴的交点
专题:
分析:(1)可先求得顶点坐标,再代入直线y=-2x+6可求得a值,可求得抛物线的解析式;
(2)由抛物线解析式可以求得B、C坐标,即可求得直线BC解析式,设直线MN解析式为y=kx+b,P(x,x+b),M(x1,x1+b),N(x2,x2+b),
即可求得PM,PN的长,可得x(x1+x2)-x1•x2-x2=2,根据M,N为x+b=-x2+2x+3上的点,即可求得x1+x2、x1•x2 的值,根据P是直线MN,BC交点,即可求得b的值,即可解题.
(2)由抛物线解析式可以求得B、C坐标,即可求得直线BC解析式,设直线MN解析式为y=kx+b,P(x,x+b),M(x1,x1+b),N(x2,x2+b),
即可求得PM,PN的长,可得x(x1+x2)-x1•x2-x2=2,根据M,N为x+b=-x2+2x+3上的点,即可求得x1+x2、x1•x2 的值,根据P是直线MN,BC交点,即可求得b的值,即可解题.
解答:解:(1)∵y=ax2-2ax-2a+1=a(x-1)2-3a+1,
∴顶点坐标为(1,-3a+1),
又∵顶点在直线y=-2x+6上,
∴-3a+1=-2+6,
解得a=-1.
∴抛物线的解析式为y=-x2+2x+3;
(2)由(1)可知抛物线为y=-x2+2x+3,
∴可求得C(0,3),B(3,0),
设直线BC解析式为y=kx+3,把B点坐标代入可求得k=-1,
∴直线BC的解析式为y=-x+3,
∴直线MN斜率为1,
设直线MN解析式为y=x+b,P(x,x+b),M(x1,x1+b),N(x2,x2+b),
则PM=
=
(x-x1 ),
PN=
=
(x2-x),
∵PM•PN=4,
∴
(x-x1 )•
(x2-x)=4,即(x-x1 )•(x2-x)=2,
展开得:x(x1+x2)-x1•x2-x2=2,
∵x1、x2 均为x+b=-x2+2x+3上的点,
∴x1+x2=-
=1,x1•x2=
=b-3,
∴x+3-b-x2=2,整理得:x2-x+b-1=0,
解得:x=
(1±
),
∵P点位于B、C两点之间,
∴x>0,
∴x=
(1+
),
∵P是直线MN,BC交点,
∴
(1+
)+b=-
(1+
)+3,
整理得:b2=1,
∴b=1或-1,
当b=1时,交点P坐标为(
,
),
b=-1时,交点P坐标为(
,
),
∴P点坐标为(
,
)或(
,
).
∴顶点坐标为(1,-3a+1),
又∵顶点在直线y=-2x+6上,
∴-3a+1=-2+6,
解得a=-1.
∴抛物线的解析式为y=-x2+2x+3;
(2)由(1)可知抛物线为y=-x2+2x+3,
∴可求得C(0,3),B(3,0),
设直线BC解析式为y=kx+3,把B点坐标代入可求得k=-1,
∴直线BC的解析式为y=-x+3,
∴直线MN斜率为1,
设直线MN解析式为y=x+b,P(x,x+b),M(x1,x1+b),N(x2,x2+b),
则PM=
| (x-x1)2+(x+b-x1-b)2 |
| 2 |
PN=
| (x2-x)2+(x2+b-x-b)2 |
| 2 |
∵PM•PN=4,
∴
| 2 |
| 2 |
展开得:x(x1+x2)-x1•x2-x2=2,
∵x1、x2 均为x+b=-x2+2x+3上的点,
∴x1+x2=-
| b |
| a |
| c |
| a |
∴x+3-b-x2=2,整理得:x2-x+b-1=0,
解得:x=
| 1 |
| 2 |
| 5-4b |
∵P点位于B、C两点之间,
∴x>0,
∴x=
| 1 |
| 2 |
| 5-4b |
∵P是直线MN,BC交点,
∴
| 1 |
| 2 |
| 5-4b |
| 1 |
| 2 |
| 5-4b |
整理得:b2=1,
∴b=1或-1,
当b=1时,交点P坐标为(
| 5 |
| 3 |
| 8 |
| 3 |
b=-1时,交点P坐标为(
| 7 |
| 3 |
| 4 |
| 3 |
∴P点坐标为(
| 5 |
| 3 |
| 8 |
| 3 |
| 7 |
| 3 |
| 4 |
| 3 |
点评:本题考查了抛物线顶点的求解,考查了抛物线对称轴的求解,考查了一次函数的综合应用,考查了直线交点的求解,本题中求PM,PM的长是解题的关键.

练习册系列答案
相关题目
下列选项正确的是( )
| A、7.93精确到个位是8.0 |
| B、42.3万精确到千分位 |
| C、42.3万精确到千位 |
| D、42.3万精确到十分位 |
已知最简二次根式
与
可以合并,则a的值是( )
| 3a-2 |
| 10a-16 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
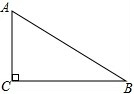 如图,在△ABC中,∠C=90°,AC=5cm,AB=10cm,以C为圆心作图,当半径r为多长时:
如图,在△ABC中,∠C=90°,AC=5cm,AB=10cm,以C为圆心作图,当半径r为多长时: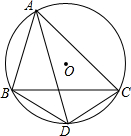 如图三角形ABC内接于⊙O,∠BAC的平分线交⊙O于点D,若∠BAC=60°.
如图三角形ABC内接于⊙O,∠BAC的平分线交⊙O于点D,若∠BAC=60°.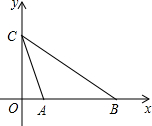 如图,平面直角坐标系中,A、B在x轴上,A(2,0)、B(8,0),点C为y轴上一动点,当∠ACB最大时,C点坐标为
如图,平面直角坐标系中,A、B在x轴上,A(2,0)、B(8,0),点C为y轴上一动点,当∠ACB最大时,C点坐标为 如图,△ABC中,D是AB上一点,AD=AC,BC边上的中线AE交CD于F,
如图,△ABC中,D是AB上一点,AD=AC,BC边上的中线AE交CD于F, 如图,在△ABC中,
如图,在△ABC中,