题目内容
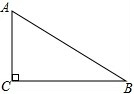 如图,在△ABC中,∠C=90°,AC=5cm,AB=10cm,以C为圆心作图,当半径r为多长时:
如图,在△ABC中,∠C=90°,AC=5cm,AB=10cm,以C为圆心作图,当半径r为多长时:(1)AB与⊙C相切;
(2)AB与⊙C相交;
(3)AB与⊙C相离.
考点:直线与圆的位置关系
专题:
分析:根据题意可求得直角三角形斜边上的高,再根据直线和圆的位置关系,判断圆心到直线AB的距离的大小关系.
解答:解:由勾股定理得BC=5
cm,再根据三角形的面积公式得,5×5
=10×斜边上的高,
∴斜边上的高=
,
(1)∵AB与⊙C相切,
∴r=
.
(2)∵AB与⊙C相交,
∴r>
.
(3)∵AB与⊙C相离,
∴r<
.
| 3 |
| 3 |
∴斜边上的高=
5
| ||
| 2 |
(1)∵AB与⊙C相切,
∴r=
5
| ||
| 2 |
(2)∵AB与⊙C相交,
∴r>
5
| ||
| 2 |
(3)∵AB与⊙C相离,
∴r<
5
| ||
| 2 |
点评:本题考查了直线和园的位置关系,判断直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.
①直线l和⊙O相交?d<r
②直线l和⊙O相切?d=r
③直线l和⊙O相离?d>r.
①直线l和⊙O相交?d<r
②直线l和⊙O相切?d=r
③直线l和⊙O相离?d>r.

练习册系列答案
相关题目
若ab<0,a+b<0,那么a、b必有( )
| A、符号相反 |
| B、符号相反且绝对值相等 |
| C、符号相反且负数的绝对值大 |
| D、符号相反且正数的绝对值大 |
已知
-
=
,则
的值是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| a-b |
| ab |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
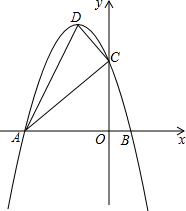 抛物线y=ax2+bx+c对称轴为直线x=-1,与x轴交于A(-3,0),B两点,与y轴交于点C(0,3),设抛物线的顶点为D.
抛物线y=ax2+bx+c对称轴为直线x=-1,与x轴交于A(-3,0),B两点,与y轴交于点C(0,3),设抛物线的顶点为D. (1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;
(1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;