题目内容
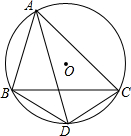 如图三角形ABC内接于⊙O,∠BAC的平分线交⊙O于点D,若∠BAC=60°.
如图三角形ABC内接于⊙O,∠BAC的平分线交⊙O于点D,若∠BAC=60°.(1)BC与BD满足什么数量关系?写出结论,并证明.
(2)AB,AC,AD之间满足什么数量关系写?出结论并证明.(最后一问要选择不同证明方法证明)
考点:圆周角定理,全等三角形的判定与性质
专题:
分析:(1)根据角平分线和圆周角定理可知BD=CD,连接OD,则OD是BC的垂直平分线,利用勾股定理可找到BD和BC之间的关系;
(2)如图2,作辅助线;证明△ADM≌△ADC,得到BM=CN;进而得到AM与AB、AC之间的数量关系,即可解决问题.
(2)如图2,作辅助线;证明△ADM≌△ADC,得到BM=CN;进而得到AM与AB、AC之间的数量关系,即可解决问题.
解答:解:(1)BC=
BD,证明如下:
∵AC平分∠BAC,∠BAC=60°,
∴∠BAD=∠BCD=∠CAD=∠DBC=30°,
∴BD=CD,
如图1,连接OD交BC于点E,则OD⊥BC,且BE=CE,

在Rt△BDE中可得cos∠EBD=
=
,
同理可得
=
,
∴
+
=
,即
=
,
∴BC=
BD;
(2)AB+AC=
AD,证明如下:
方法一:如图2,过点D作DN⊥AC于点N,

DM⊥AB,交AB的延长线于点M;
∵AD平分∠BAC,
∴DM=DN,BD=CD,∠MAD=∠NAD(设为α),
∵cosα=
=
,
∴AM=AN;
∵∠MBD=∠NCD(设为β),
∴cosβ=
=
,而BD=CD,
∴BM=NC(设为λ),
∴AB+λ=AC-λ,
∴λ=
,AM=AB+λ=
;
∵cos30°=
,
∴AM=
AD,
∴AB+AC=
AD.
方法二,
如图3,延长AB到M,使AM=AC;

过点D作DN⊥BM于点N;
在△ADM与△ADC中,
,
∴△ADM≌△ADC(SAS),
∴DM=DC;由(1)知:BD=DC,
∴DM=DB,MN=BN=
,
∴AN=AB+BN=
,
∴cos30°=
,AN=
AD,
∴AB+AC=
AD.
| 3 |
∵AC平分∠BAC,∠BAC=60°,
∴∠BAD=∠BCD=∠CAD=∠DBC=30°,
∴BD=CD,
如图1,连接OD交BC于点E,则OD⊥BC,且BE=CE,

在Rt△BDE中可得cos∠EBD=
| BE |
| BD |
| ||
| 2 |
同理可得
| CE |
| CD |
| ||
| 2 |
∴
| CE |
| CD |
| BE |
| BD |
| 3 |
| BC |
| BD |
| 3 |
∴BC=
| 3 |
(2)AB+AC=
| 3 |
方法一:如图2,过点D作DN⊥AC于点N,

DM⊥AB,交AB的延长线于点M;
∵AD平分∠BAC,
∴DM=DN,BD=CD,∠MAD=∠NAD(设为α),
∵cosα=
| AM |
| AD |
| AN |
| AD |
∴AM=AN;
∵∠MBD=∠NCD(设为β),
∴cosβ=
| BM |
| BD |
| NC |
| DC |
∴BM=NC(设为λ),
∴AB+λ=AC-λ,
∴λ=
| AC-AB |
| 2 |
| AB+AC |
| 2 |
∵cos30°=
| AM |
| AD |
∴AM=
| ||
| 2 |
∴AB+AC=
| 3 |
方法二,
如图3,延长AB到M,使AM=AC;

过点D作DN⊥BM于点N;
在△ADM与△ADC中,
|
∴△ADM≌△ADC(SAS),
∴DM=DC;由(1)知:BD=DC,
∴DM=DB,MN=BN=
| AC-AB |
| 2 |
∴AN=AB+BN=
| AB+AC |
| 2 |
∴cos30°=
| AN |
| AD |
| ||
| 2 |
∴AB+AC=
| 3 |
点评:该题主要考查了圆周角定理及其推论、全等三角形的判定及其性质等几何知识点的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列运算中,结果正确的是( )
| A、a2+a2=a4 | ||
| B、a3×a=a4 | ||
C、3a-1=
| ||
| D、(-2a2)3=-6a6 |
 (1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;
(1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;