题目内容
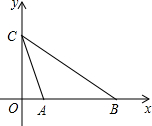 如图,平面直角坐标系中,A、B在x轴上,A(2,0)、B(8,0),点C为y轴上一动点,当∠ACB最大时,C点坐标为
如图,平面直角坐标系中,A、B在x轴上,A(2,0)、B(8,0),点C为y轴上一动点,当∠ACB最大时,C点坐标为考点:切线的性质,坐标与图形性质,圆周角定理
专题:计算题
分析:根据圆周角定理,当过A、B两点的⊙P与y轴正半轴相切于C时,∠ACB最大时,作PH⊥AB于H,连结PC、PA,如图先得到OA=2,AB=6,根据垂径定理得AH=BH=3,则OH=OA+AH=5,再利用切线的性质得PC⊥y轴,则四边形PHOC为矩形,所以OC=PH,PC=OH=5,在Rt△PAH中利用勾股定理计算出PH=4,则OC=4,所以C点坐标为(4,0),同理可得当⊙P与y轴的负半轴相切时,C点坐标为(-4,0).
解答:解:当过A、B两点的⊙P与y轴正半轴相切于C时,∠ACB最大时,
作PH⊥AB于H,连结PC、PA,如图,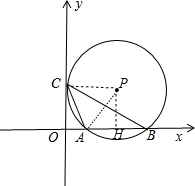
∵A(2,0)、B(8,0),
∴OA=2,AB=6,
∵PH⊥AB,
∴AH=BH=3,
∴OH=OA+AH=5,
∵⊙P与y轴相切,
∴PC⊥y轴,
∴四边形PHOC为矩形,
∴OC=PH,PC=OH=5,
在Rt△PAH中,∵AH=3,PA=5,
∴PH=
=4,
∴OC=4,
∴C点坐标为(4,0),
当⊙P与y轴的负半轴相切时,C点坐标为(-4,0).
故答案为(4,0)或(-4,0).
作PH⊥AB于H,连结PC、PA,如图,

∵A(2,0)、B(8,0),
∴OA=2,AB=6,
∵PH⊥AB,
∴AH=BH=3,
∴OH=OA+AH=5,
∵⊙P与y轴相切,
∴PC⊥y轴,
∴四边形PHOC为矩形,
∴OC=PH,PC=OH=5,
在Rt△PAH中,∵AH=3,PA=5,
∴PH=
| PA2-AH2 |
∴OC=4,
∴C点坐标为(4,0),
当⊙P与y轴的负半轴相切时,C点坐标为(-4,0).
故答案为(4,0)或(-4,0).
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了坐标与图形性质.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知
-
=
,则
的值是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| a-b |
| ab |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
下列运算中,结果正确的是( )
| A、a2+a2=a4 | ||
| B、a3×a=a4 | ||
C、3a-1=
| ||
| D、(-2a2)3=-6a6 |
 (1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;
(1)已知抛物线y=ax2-2ax-2a+1分别交x轴于A、B两点,交y轴于C点,其顶点在直线y=-2x+6上,求抛物线的解析式;