题目内容
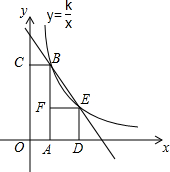 如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=
如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=| k |
| x |
(1)求反比例函数的表达式;
(2)求正方形ADEF的边长;
(3)根据图象直接写出直线BE对应的一次函数的函数值大于反比例函数y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据OA和OC的长即可求得B的坐标,利用待定系数法求得反比例函数解析式;
(2)根据正方形的性质,设正方形ADEF的边长AD=t,则OD=1+t,则E点坐标为(1+t,t).代入反比例函数解析式即可求得t的值,得到正方形的边长;
(3)直线BE对应的一次函数的函数值大于反比例函数y=
的值,即对应相同的x的值时,一次函数对应的点在反比例函数的图象的点的上边,据此即可判断.
(2)根据正方形的性质,设正方形ADEF的边长AD=t,则OD=1+t,则E点坐标为(1+t,t).代入反比例函数解析式即可求得t的值,得到正方形的边长;
(3)直线BE对应的一次函数的函数值大于反比例函数y=
| k |
| x |
解答:解:(1)∵OA=1,OB=6,
∴B点的坐标为(1,6).
∵点B在反比例函数y=
的图象上,
∴k=1×6=6.
∴所求的反比例函数表达式为y=
.
(2)设正方形ADEF的边长AD=t,则OD=1+t.
∵四边形ADEF是正方形,
∴DE=AD=t.
∴E点坐标为(1+t,t).
∵E点在反比例函数y=
的图象上,
∴(1+t)•t=6.
整理,得 t2+t-6=0.
解得t1=-3,t2=2.
∵t>0,
∴t=2.
∴正方形ADEF的边长为2.
(3)1<x<3或x<0.
∴B点的坐标为(1,6).
∵点B在反比例函数y=
| 6 |
| x |
∴k=1×6=6.
∴所求的反比例函数表达式为y=
| 6 |
| x |
(2)设正方形ADEF的边长AD=t,则OD=1+t.
∵四边形ADEF是正方形,
∴DE=AD=t.
∴E点坐标为(1+t,t).
∵E点在反比例函数y=
| 6 |
| x |
∴(1+t)•t=6.
整理,得 t2+t-6=0.
解得t1=-3,t2=2.
∵t>0,
∴t=2.
∴正方形ADEF的边长为2.
(3)1<x<3或x<0.
点评:本题主要考查了正方形的性质和待定系数法求反比例函数与一次函数的解析式.这里体现了数形结合的思想.

练习册系列答案
相关题目
已知二次函数y=x2-2x+1,当y=4时,x的值等于( )
| A、3和-1 | B、-3和1 |
| C、3和1 | D、-3和-1 |
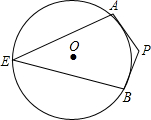 如图,PA,PB分别切⊙O于点A、B,点E是⊙O上一点,若∠AEB=40°,求∠APB的度数.
如图,PA,PB分别切⊙O于点A、B,点E是⊙O上一点,若∠AEB=40°,求∠APB的度数.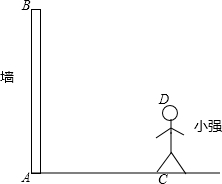 某一时刻身高为1.5m的小强CD在太阳光下的影长为2m,学校有一堵墙AB高为3m,如图所示,此刻小强行走在院墙内,若不想被太阳光照射到,请通过计算说明小强可以走动的范围.
某一时刻身高为1.5m的小强CD在太阳光下的影长为2m,学校有一堵墙AB高为3m,如图所示,此刻小强行走在院墙内,若不想被太阳光照射到,请通过计算说明小强可以走动的范围.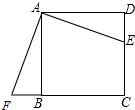 如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.
如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.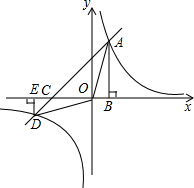 如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数y=
如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数y= 在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=