题目内容
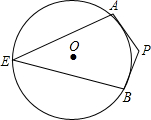 如图,PA,PB分别切⊙O于点A、B,点E是⊙O上一点,若∠AEB=40°,求∠APB的度数.
如图,PA,PB分别切⊙O于点A、B,点E是⊙O上一点,若∠AEB=40°,求∠APB的度数.考点:切线的性质
专题:
分析:连接OA,BO,由圆周角定理知可知∠AOB=2∠E=80°,PA、PB分别切⊙O于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠P=180°-∠AOB=100°.
解答: 解:连接OA,BO;
解:连接OA,BO;
∵∠AOB=2∠E=80°,
∴∠OAP=∠OBP=90°,
∴∠APB=180°-∠AOB=100°.
 解:连接OA,BO;
解:连接OA,BO;∵∠AOB=2∠E=80°,
∴∠OAP=∠OBP=90°,
∴∠APB=180°-∠AOB=100°.
点评:本题考查了切线的性质,圆周角定理,四边形的内角和为360度等,熟练掌握切线的性质和圆心角与圆周角的关系是关键.

练习册系列答案
相关题目
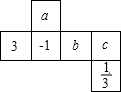 如图是一个正方体纸盒的展开图,每个面用相应的数字或字母表示,若把它围成正方体后,a与它对面的数的积等于1,b与它对面的数的和等于0,c的绝对值与它对面的数的绝对值相等,则(a+b)c的值等于( )
如图是一个正方体纸盒的展开图,每个面用相应的数字或字母表示,若把它围成正方体后,a与它对面的数的积等于1,b与它对面的数的和等于0,c的绝对值与它对面的数的绝对值相等,则(a+b)c的值等于( )| A、0 | B、6 | C、-6 | D、6或-6 |
已知一个二元一次方程组的解是
,则这个方程组是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 小明不慎将一块三角形的玻璃打碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带
小明不慎将一块三角形的玻璃打碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带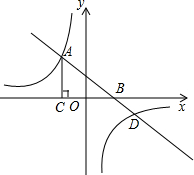 如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y= 某旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB的边缘上建一个休息点M,使它到A,C两个点的距离相等.在图中确定休息点M的位置.
某旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB的边缘上建一个休息点M,使它到A,C两个点的距离相等.在图中确定休息点M的位置. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,若点A(4,0)在该抛物线上,则4a-2b+c的值为
如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,若点A(4,0)在该抛物线上,则4a-2b+c的值为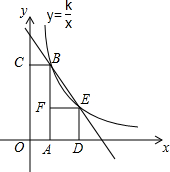 如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=
如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=