题目内容
19.抛物线y=4x2-2ax+b与x轴相交于A(x1,0),B(x2,0)(0<x1<x2)两点,与y轴交于点C.(1)设AB=2,tan∠ABC=4,求该抛物线的解析式;
(2)在(1)中,若点D为直线BC下方抛物线上一动点,当△BCD的面积最大时,求点D的坐标;
(3)是否存在整数a,b使得1<x1<2和1<x2<2同时成立,请证明你的结论.
分析 (1)由tan∠ABC=4,可以假设B(m,0),则A(m-2,0),C(0,4m),可得抛物线的解析式为y=4(x-m)(x-m+2),把C(0,4m)代入y=4(x-m)(x-m+2),求出m的值即可解决问题;
(2)设P(m,4m2-16m+12).作PH∥OC交BC于H,根据S△PBC=S△PHC+S△PHB构建二次函数,利用二次函数的性质解决问题;
(3)不存在.假设存在,由题意由题意可知,$\left\{\begin{array}{l}{4-2a+b>0}\\{16-4a+b>0}\\{4{a}^{2}-16b>0}\end{array}\right.$且1<-$\frac{-2a}{8}$<2,首先求出整数a的值,代入不等式组,解不等式组即可解决问题.
解答 解:(1)∵tan∠ABC=4
∴可以假设B(m,0),则A(m-2,0),C(0,4m),
∴可以假设抛物线的解析式为y=4(x-m)(x-m+2),
把C(0,4m)代入y=4(x-m)(x-m+2),得m=3,
∴抛物线的解析式为y=4(x-3)(x-1),
∴y=4x2-16x+12,
(2)如图,设D(m,4m2-16m+12).作DH∥OC交BC于H.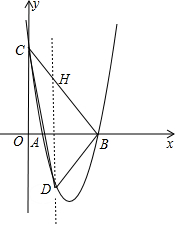
∵B(3,0),C(0,12),
∴直线BC的解析式为y=-4x+12,
∴H(m,-4m+12),
∴S△DBC=S△DHC+S△DHB=$\frac{1}{2}$•(-4m+12-4m2+16m-12)•3=-6(m-$\frac{3}{2}$)2+$\frac{27}{2}$,
∵-6<0,
∴m=$\frac{3}{2}$时,△DBC面积最大,
此时D($\frac{3}{2}$,-3).
(3)不存在.
理由:假设存在.由题意可知,
$\left\{\begin{array}{l}{4-2a+b>0}\\{16-4a+b>0}\\{4{a}^{2}-16b>0}\end{array}\right.$且1<-$\frac{-2a}{8}$<2,
∴4<a<8,
∵a是整数,
∴a=5 或6或7,
当a=5时,代入不等式组,不等式组无解.
当a=6时,代入不等式组,不等式组无解.
当a=7时,代入不等式组,不等式组无解.
综上所述,不存在整数a、b,使得1<x1<2和1<x2<2同时成立.
点评 本题考查二次函数综合题、待定系数法、三角形的面积,不等式组等整数,解题的关键是灵活运用待定系数法确定函数解析式,学会构建二次函数,利用二次函数的性质解决问题,学会利用不等式组解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 正方形 | B. | 正六边形 | C. | 正八边形 | D. | 正十二边形 |
| A. | (3,-2) | B. | (1,-6) | C. | (-1,6) | D. | (-1,-6) |
| A. | sinA=$\frac{c}{a}$ | B. | cosB=$\frac{b}{c}$ | C. | sinB=$\frac{b}{a}$ | D. | tanA=$\frac{a}{b}$ |
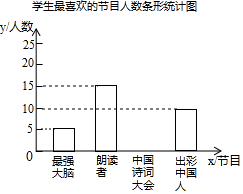 为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:学生最喜爱的节目人数统计表
| 节目 | 人数(名) | 百分比 |
| 最强大脑 | 5 | 10% |
| 朗读者 | 15 | b% |
| 中国诗词大会 | a | 40% |
| 出彩中国人 | 10 | 20% |
(1)x=50,a=20,b=30;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 9.14 | 9.15 | 9.14 | 9.15 |
| 方差 | 6.6 | 6.8 | 6.7 | 6.6 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |