题目内容
14.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过P(-2,3),则该函数不经过的图象的点是( )| A. | (3,-2) | B. | (1,-6) | C. | (-1,6) | D. | (-1,-6) |
分析 先求出函数的解析式,再代入看看两边是否相等即可.
解答 解:∵反比例函数y=$\frac{k}{x}$(k≠0)的图象经过P(-2,3),
∴代入得:3=$\frac{k}{-2}$,
解得:k=-6,
即y=-$\frac{6}{x}$,
A、∵把(3,-2)代入y=-$\frac{6}{x}$时,左边=右边,
∴点(3,-2)在函数y=-$\frac{6}{x}$的图象上,故本选项不符合题意;
B、∵把(1,-6)代入y=-$\frac{6}{x}$时,左边=右边,
∴点(1,-6)在函数y=-$\frac{6}{x}$的图象上,故本选项不符合题意;
C、∵把(-1,6)代入y=-$\frac{6}{x}$时,左边=右边,
∴点(-1,6)在函数y=-$\frac{6}{x}$的图象上,故本选项不符合题意;
D、∵把(-1,-6)代入y=-$\frac{6}{x}$时,左边≠右边,
∴点(-1,-6)在函数y=-$\frac{6}{x}$的图象上,故本选项符合题意;
故选D.
点评 本题考查了反比例函数图象上点的坐标特征,用待定系数法求函数的解析式等知识点,能理解反比例函数图象上点的特点是解此题的关键.

练习册系列答案
相关题目
5.已知下列命题:
①各边相等的多边形是正多边形;
②相等的圆心角所对的弧相等;
③若a2=b2,则a=b;
④若直线y=kx+b经过第一、二、四象限,则k<0,b>0.
其中原命题与逆命题都是真命题的个数是( )
①各边相等的多边形是正多边形;
②相等的圆心角所对的弧相等;
③若a2=b2,则a=b;
④若直线y=kx+b经过第一、二、四象限,则k<0,b>0.
其中原命题与逆命题都是真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.某企业今年3月份产值为m万元,4月份比3月份减少了8%,预测5月份比4月份增加9%,则5月份的产值是( )
| A. | (m-8%)(m+9%)万元 | B. | (1-8%)(1+9%)m万元 | C. | (m-8%+9%)万元 | D. | (m-8%+9%)m万元 |
9.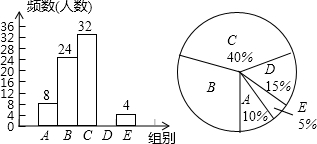 今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
(1)表中的n=12,中位数落在C组,扇形统计图中B组对应的圆心角为108°;
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
 今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题| 组别 | 学习时间x(h) | 频数(人数) |
| A | 0<x≤1 | 8 |
| B | 1<x≤2 | 24 |
| C | 2<x≤3 | 32 |
| D | 3<x≤4 | n |
| E | 4小时以上 | 4 |
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
3. 如图所示的几何体是由五个小正方体组成的,它的左视图是( )
如图所示的几何体是由五个小正方体组成的,它的左视图是( )
 如图所示的几何体是由五个小正方体组成的,它的左视图是( )
如图所示的几何体是由五个小正方体组成的,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.