Question

20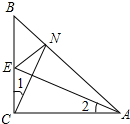．如图，△ABC中，∠CAB=∠CBA=45°，CA=CB，点E为BC的中点，CN⊥AE交AB于N．
（1）求证：∠1=∠2；
（2）求证：AE=CN+EN．（请用多种方法证明）
（一）直接截长法
（二）间接截长法
（三）直接补短法
（四）间接补短法．

Answer 1

分析 （1）根据同角的余角相等即可证明．
（2）证法一（直接截长法）：如图2中，在线段AE上截取AM=CN，连接CM．
证法二（间接截长法）：如图2中，作CM平分∠ACB交AE于M．
证法三（直接补短法）如图3中，延长CN到M，使得CM=AE．
证法四（间接补短法），如图3中，作BM⊥BC，交CN于M．

解答 证明：（1）如图1中，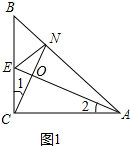

∵∠CAB=∠CBA=45°，
∴∠ACB=90°，
∵AE⊥CN，
∴∠AOC=90°，
∴∠1+∠ACO=90°，∠2+∠ACO=90°，
∴∠1=∠2．

（2）证法一（直接截长法）：如图2中，在线段AE上截取AM=CN，连接CM．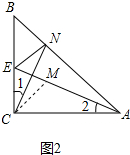

在△ACM和△CBN中，
$\left\{\begin{array}{l}{AC=BC}\\{∠1=∠2}\\{AM=CN}\end{array}\right.$，
∴△ACM≌△CBN，
∴CM=BN，∠ACM=∠B=45°，
∴∠MCE=45°，
∴∠B=∠MCE，
在△MCE和△NBE中，
$\left\{\begin{array}{l}{CM=BN}\\{∠MCB=∠B}\\{CE=BE}\end{array}\right.$，
∴△MCE≌△NBE，
∴EM=EN，
∴AE=AM+EM=CN+EN．

证法二（间接截长法）：如图2中，作CM平分∠ACB交AE于M．
在△ACM和△CBN中，
$\left\{\begin{array}{l}{∠1=∠2}\\{AC=BC}\\{∠ACM=∠B}\end{array}\right.$，
∴△ACM≌△CBN，
∴CM=BN，∠ACM=∠B=45°，
∴∠MCE=45°，
∴∠B=∠MCE，
在△MCE和△NBE中，
$\left\{\begin{array}{l}{CM=BN}\\{∠MCB=∠B}\\{CE=BE}\end{array}\right.$，
∴△MCE≌△NBE，
∴EM=EN，
∴AE=AM+EM=CN+EN．

证法三（直接补短法）如图3中，延长CN到M，使得CM=AE．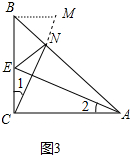

在△ACE和△CBM中，
$\left\{\begin{array}{l}{∠1=∠2}\\{∠ACE=∠CBM}\\{AC=BC}\end{array}\right.$，
∴△ACE≌△CBE，
∴CE=BM=BE，∠ACE=∠CBM=90°，
∴∠MBN=45°=∠NBE，
在△NBM和△NBE中，
$\left\{\begin{array}{l}{BN=BN}\\{∠NBM=∠NBE}\\{BM=BE}\end{array}\right.$，
∴△NBM≌△NBE，
∴NM=EN，
∴AE=CM=CN+NM=CN+EN．
证法四（间接补短法），如图3中，作BM⊥BC，交CN于M．
在△ACE和△CBM中，
$\left\{\begin{array}{l}{∠1=∠2}\\{BC=AC}\\{∠CBM=∠ACE}\end{array}\right.$，
∴△ACE≌△CBE，
∴CE=BM=BE，
∵∠CBM=90°，∠CBA=45°，
∴∠NBM=∠NBE=45°
在△NBM和△NBE中，
$\left\{\begin{array}{l}{BN=BN}\\{∠NBM=∠NBE}\\{BM=BE}\end{array}\right.$，
∴△NBM≌△NBE，
∴NM=EN，
∴AE=CM=CN+NM=CN+EN．

点评 本题考查全等三角形的判定和性质，解题的关键是学会添加常用辅助线，构造全等三角形，属于中考常考题型．