题目内容
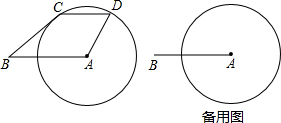
9.已知:如图,线段AB=8,以A为圆心,5为半径作圆A,点C在⊙A上,过点C作CD∥AB交⊙A于点D(点D在C右侧),联结BC、AD.(1)若CD=6,求四边形ABCD的面积;
(2)设CD=x,BC=y,求y与x的关系式及x的取值范围;
(3)设BC的中点为M,AD的中点为N,MN∥CD,线段MN交⊙A于点E,联结CE,当CD取何值时,CE∥AD.
分析 (1)作AH⊥CD于H,如图1,根据垂径定理得到CH=DH=3,再利用勾股定理计算出AH,然后根据梯形的面积公式求解;
(2)作CP⊥AB于P,连接AC,如图1,根据垂径定理得CH=DH=$\frac{1}{2}$CD=$\frac{1}{2}$x,易得四边形AHCP为矩形,则AP=CH=$\frac{1}{2}$x,所以BP=AB-AP=8-$\frac{1}{2}$x,于是利用勾股定理可表示出CP2=25-$\frac{1}{4}$x2,然后在Rt△BPC中利用勾股定理可表示出y与x的关系式;
(3)作AH⊥CD于H,交MN于点F,连结AE,如图2,先证明四边形CEND为平行四边形得到DC=NE,设CD=x,则NE=x,再说明FN为△AHD的中位线得到FN=$\frac{1}{2}$DH=$\frac{1}{4}$x,则EF=$\frac{3}{4}$x,接着利用勾股定理得到AE2-EF2=AN2-NF2,即52-($\frac{3}{4}$x)2=($\frac{5}{2}$)2-($\frac{1}{4}$x)2,然后解方程求出x即可.
解答 解:(1)作AH⊥CD于H,如图1,则CH=DH=$\frac{1}{2}$CD=$\frac{1}{2}$×6=3,
在Rt△AHD中,∵AD=5,DH=3,
∴AH=$\sqrt{{5}^{2}-{3}^{2}}$=4,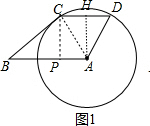
∴四边形ABCD的面积=$\frac{1}{2}$(CD+AB)•AH=$\frac{1}{2}$×(6+8)×4=28;
(2)作CP⊥AB于P,连接AC,如图1,
∵AH⊥CD,
∴CH=DH=$\frac{1}{2}$CD=$\frac{1}{2}$x,
易得四边形AHCP为矩形,
∴AP=CH=$\frac{1}{2}$x,
∴BP=AB-AP=8-$\frac{1}{2}$x,
在Rt△PAC中,∵AC2=AP2+CP2,
∴CP2=25-$\frac{1}{4}$x2,
在Rt△BPC中,∵BC2=BP2+CP2,
∴y2=(8-$\frac{1}{2}$x)2+25-$\frac{1}{4}$x2=89-8x,
∴y=$\sqrt{89-8x}$(0<x<10);
(3)作AH⊥CD于H,交MN于点F,连结AE,如图2,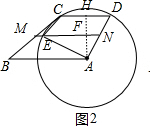
∵MN∥CD,CE∥AD,
∴四边形CEND为平行四边形,
∴DC=NE,
设CD=x,则NE=x,
∵FN∥CD,N点为AD的中点,
∴FN为△AHD的中位线,
∴FN=$\frac{1}{2}$DH=$\frac{1}{4}$x,
∴EF=x-$\frac{1}{4}$x=$\frac{3}{4}$x,
在Rt△AEF中,AF2=AE2-EF2,
在Rt△AFN中,AF2=AN2-NF2,
∴AE2-EF2=AN2-NF2,即52-($\frac{3}{4}$x)2=($\frac{5}{2}$)2-($\frac{1}{4}$x)2,解得x=$\frac{5\sqrt{6}}{2}$,
即当CD为$\frac{5\sqrt{6}}{2}$时,CE∥AD.
点评 本题考查了圆的综合题:熟练掌握垂径定理和平行四边形的判定与性质;会利用勾股定理计算线段的长和表示线段之间的关系.过圆心作弦的垂线段和作梯形的高为常见的辅助线.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案 如图所示几何体的左视图是( )
如图所示几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
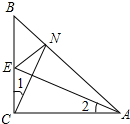 如图,△ABC中,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.
如图,△ABC中,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.