题目内容
20.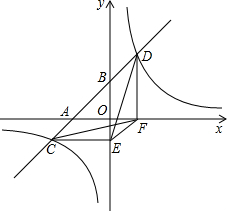 如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:①△DCE≌△CDF;
②△AOB∽△FOE;
③△CEF与△DEF的面积相等;
④AC=BD.
其中正确的有①②③④.(只填写序号)
分析 先求出A、B、C、D四点坐标,再由DF⊥x轴,CE⊥y轴即可得出CE及DF的长,故可得出①正确;利用待定系数法求出直线EF的解析式,根据解析式的系数可判断出AB∥EF,再由相似三角形的判定定理可得出②正确;根据同底等高的三角形面积相等可知③正确;根据两点间的距离公式求出AC及BD的长可知④正确.
解答 解:∵一次函数y=x+3的图象与轴,y轴交于A,B两点,
∴A(-3,0),B(0,3).
∵与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,
∴$\left\{\begin{array}{l}y=x+3\\ y=\frac{4}{x}\end{array}\right.$,解得$\left\{\begin{array}{l}x=-4\\ y=-1\end{array}\right.$或$\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$,
∴C(-4,-1),D(1,4).
∵DF⊥x轴,CE⊥y轴,
∴E(0,-1),F(1,0),
∴CE=DF=4,CF=DE=$\sqrt{{(-4-1)}^{2}+{(-1-0)}^{2}}$=$\sqrt{26}$.
在DCE与△CDF中,
∵$\left\{\begin{array}{l}CD=CD\\ CE=DF\\ CF=DE\end{array}\right.$
∴△DCE≌△CDF(SSS),故①正确;
设直线EF的解析式为y=mx+n(m≠0),
∵E(0,-1),F(1,0),
∴$\left\{\begin{array}{l}n=-1\\ m+n=0\end{array}\right.$,解得$\left\{\begin{array}{l}n=-1\\ m=1\end{array}\right.$,
∴直线EF的解析式为y=x-1.
∵直线AB的解析式为:y=x+3,
∴AB∥EF,
∴∠FEO=∠ABO,∠EFO=∠BAO,
∴△AOB∽△FOE,故②正确;
∵EF∥AB,
∴△CEF与△DEF同底等高,
∴△CEF与△DEF的面积相等,故③正确;
∵A(-3,0),B(0,3),C(-4,-1),D(1,4),
∴AC=$\sqrt{(-3+4)^{2}+{1}^{2}}$=$\sqrt{2}$,BD=$\sqrt{{1}^{2}+(3-4)^{2}}$=$\sqrt{2}$,
∴AC=BD,即④正确.
故答案为:①②③④.
点评 本题考查的是反比例函数函数综合题,涉及到一次函数图象上点的坐标特点、反比例函数与一次函数的交点问题、全等三角形及相似三角形的判定等知识,涉及面较广.

 如图,点A在直线l上,请在直线l上另找一点C,使△ABC是等腰三角形.请找出所有符合条件的点(保留作图痕迹).
如图,点A在直线l上,请在直线l上另找一点C,使△ABC是等腰三角形.请找出所有符合条件的点(保留作图痕迹).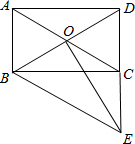 如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E. 如图,直线l切⊙O于点A,点B是l上的点,连结BO并延长,交⊙O于点C,连结AC,若∠C=25°,则∠ABC等于40°.
如图,直线l切⊙O于点A,点B是l上的点,连结BO并延长,交⊙O于点C,连结AC,若∠C=25°,则∠ABC等于40°.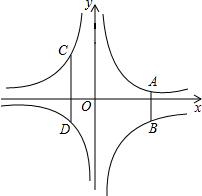 如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.
如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.