题目内容
15. 如图,直线l切⊙O于点A,点B是l上的点,连结BO并延长,交⊙O于点C,连结AC,若∠C=25°,则∠ABC等于40°.
如图,直线l切⊙O于点A,点B是l上的点,连结BO并延长,交⊙O于点C,连结AC,若∠C=25°,则∠ABC等于40°.
分析 连接OA,由切线的性质可知∠BOA=90°,再根据三角形外角和定理可求出∠BOA的度数,进而可求出∠ABC的大小.
解答 解:
∵直线l切⊙O于点A,
∴OA⊥AB,
∴∠BOA=90°,
∵OA=OC,
∴∠AOC=∠C=25°,
∴∠BOA=50°,
∴∠ABC=90°-50°=40°,
故答案为:40.
点评 本题考查了圆的切线性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
5.若m等于它的倒数,则分式$\frac{{m}^{2}-4m+4}{{m}^{2}-4}÷(m-2)$的值为( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{3}$或1 | D. | 以上都不对 |
6.下列调查中,适宜采用普查方式的是( )
| A. | 了解一批圆珠笔的寿命 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 检查一枚用于发射卫星的运载火箭的各零部件 | |
| D. | 考察人们保护海洋的意识 |
10.(-$\frac{1}{3}$)-1-4cos30°+|-$\sqrt{12}$|的计算结果为( )
| A. | -4 | B. | 4 | C. | -3 | D. | -2 |
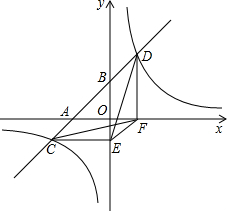 如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
如图,一次函数y=x+3的图象与轴,y轴交于A,B两点,与反比例函数y=$\frac{4}{x}$的图象相交于C,D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论: