题目内容
17. 如图,等边△OAB边长为2,点B在x轴上,将△OAB沿AB所在直线对折,得到△O'AB,则点O的对应点O'的坐标是(3,$\sqrt{3}$).
如图,等边△OAB边长为2,点B在x轴上,将△OAB沿AB所在直线对折,得到△O'AB,则点O的对应点O'的坐标是(3,$\sqrt{3}$).
分析 由折叠的性质和等边三角形的性质知OB=AO′,可先求出A点坐标,然后将A点坐标向右平移2个单位即可得到O′点的坐标.
解答  解:过A作AD⊥x轴于D;
解:过A作AD⊥x轴于D;
在Rt△OAD中,OA=2,∠AOD=60°,则:
OD=1,AD=$\sqrt{3}$;
∴A(1,$\sqrt{3}$);
由折叠的性质和等边三角形的性质知:AO′=OB=2,
∴O′的坐标是(3,$\sqrt{3}$).
故答案为:(3,$\sqrt{3}$).
点评 此题主要考查了等边三角形的性质、解直角三角形以及图象的翻折变换,能够根据折叠的性质得到AO′的长是解答此题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
7.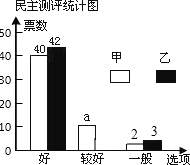 我校2017年度“春之声”歌咏比赛已正式拉开序幕,其中甲、乙两个班级的表现分外突出,现场A,B,C,D,E五位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:
我校2017年度“春之声”歌咏比赛已正式拉开序幕,其中甲、乙两个班级的表现分外突出,现场A,B,C,D,E五位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:
(1)a=8,五位评委对乙班所打分数的中位数是90,并补全条形统计图;
(2)若将评委评分中最高和最低分去掉,再算平均分,并将平均分与民意测评分按3:2计算最后得分,那么甲、乙两班谁是第一名?并说明理由.(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
 我校2017年度“春之声”歌咏比赛已正式拉开序幕,其中甲、乙两个班级的表现分外突出,现场A,B,C,D,E五位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:
我校2017年度“春之声”歌咏比赛已正式拉开序幕,其中甲、乙两个班级的表现分外突出,现场A,B,C,D,E五位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 96 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |
(2)若将评委评分中最高和最低分去掉,再算平均分,并将平均分与民意测评分按3:2计算最后得分,那么甲、乙两班谁是第一名?并说明理由.(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
7.已知$\frac{a}{5}$=$\frac{b}{3}$=k(k≠0),则$\frac{a-b}{a+b}$=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
 如图是某超市楼梯示意图,若BA与CA的夹角为α,∠C=90°,AC=6米,则楼梯高度BC为6tanα米.
如图是某超市楼梯示意图,若BA与CA的夹角为α,∠C=90°,AC=6米,则楼梯高度BC为6tanα米.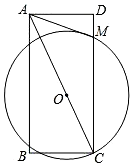 如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.
如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.