题目内容
7．已知$\frac{a}{5}$=$\frac{b}{3}$=k（k≠0），则$\frac{a-b}{a+b}$=（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{5}$ |
分析 根据比例的性质即可得到结论．
解答 解：∵$\frac{a}{5}$=$\frac{b}{3}$=k，
∴a=5k，b=3k，
∴$\frac{a-b}{a+b}$=$\frac{5k-3k}{5k+3k}$=$\frac{1}{4}$，
故选B．
点评 本题考查了比例的性质，熟练正确比例的性质即可得到结论．
练习册系列答案
相关题目
如图，等边△OAB边长为2，点B在x轴上，将△OAB沿AB所在直线对折，得到△O'AB，则点O的对应点O'的坐标是（3，$\sqrt{3}$）．
15．一家公司打算招聘一名英文翻译，对甲、乙两名应试者进行了听、说、读、写的英语水平测试，他们的各项成绩（百分制）如下：
如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照3：3：2：2的比确定，应该录取甲（填“甲”或“乙”）
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 83 | 78 | 75 |
| 乙 | 73 | 80 | 85 | 82 |
2．某水果批发商店为了考察1000筐苹果的等次，从中抽取了50筐进行检查，下面说法正确的是（ ）
| A． | 总体是1000筐苹果 | B． | 样本是50筐苹果 | ||
| C． | 总体是指1000筐苹果的等次 | D． | 样本是指苹果的等次 |
12．某班学生的期中成绩（成绩为整数）的频数分布表如下，请根据表中提供的信息回答下列问题：
（1）m=0.15，n=24，p=0.1，q=60；
（2）在表内，频率最小的一组的成绩范围是49.5-59.5．
（3）成绩优秀的学生有24人（成绩大于或等于80分为优秀）．
| 分组 | 频数 | 频率 |
| 49.5-59.5 | 3 | 0.05 |
| 59.5-69.5 | 9 | m |
| 69.5-79.5 | n | 0.40 |
| 79.5-89.5 | 18 | 0.30 |
| 89.5-99.5 | 6 | p |
| 合计 | q | 1.0 |
（2）在表内，频率最小的一组的成绩范围是49.5-59.5．
（3）成绩优秀的学生有24人（成绩大于或等于80分为优秀）．
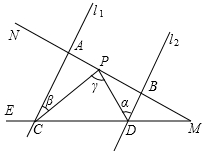如图，已知 l1∥l2，射线MN分别和直线l1，l2交于A、B，射线ME分别和直线l1，l2交于C、D，点P在A、B间运动（P与A、B两点不重合），设∠PDB=α，∠PCA=β，∠CPD=γ．