题目内容
4.直线a⊥直线b,垂足为O,点A与点A'关于直线a对称,点A'与A''关于直线b对称,点A与点A''的对称关系是:关于点O成中心对称.分析 先根据轴对称的性质得到AO=A'O=A“O,∠APA'=2α,∠A'OA“=2β,再根据α+β=90°,即可得出∠AOA“=180°,进而得出点A与点A''的对称关系.
解答  解:如图所示,连接AO,A'O,A“O,
解:如图所示,连接AO,A'O,A“O,
由轴对称的性质可得,AO=A'O=A“O,∠APA'=2α,∠A'OA“=2β,
由直线a⊥直线b,可得α+β=90°,
∴∠AOA'+∠A'OA“=180°,
即∠AOA“=180°,
∴AA“经过点O,
∴点A与点A''关于点O成中心对称.
故答案为:关于点O成中心对称.
点评 本题主要考查了轴对称与中心对称的运用,解题时注意:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.

练习册系列答案
相关题目
15.直角三角形的两个锐角平分线的夹角是( )
| A. | 45° | B. | 135° | ||
| C. | 45°或135° | D. | 由两个锐角的大小决定 |
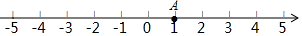 如图,在数轴上,点A表示的数是1,现将点A沿数轴做如下移动,第一次点A向左移动3 个单位长度到达点A1,点A1表示的数是-2;
如图,在数轴上,点A表示的数是1,现将点A沿数轴做如下移动,第一次点A向左移动3 个单位长度到达点A1,点A1表示的数是-2;