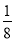题目内容
如图,在△ABD和△ACE中,AB=AD,AC=AE,∠BAD=∠CAE,连接BC、DE相交于点F,BC与AD相交于点G.
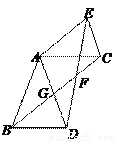
(1)试判断线段BC、DE的数量关系,并说明理由;
(2)若BC平分∠ABD,求证线段FD是线段FG 和 FB的比例中项.
(1),理由见解析; (2)证明见解析. 【解析】试题分析:(1)先判断出关系,然后根据三角形全的判定SAS证明△BAC≌△DAE即可; (2)根据条件证明△DFG∽△BFD,利用相似三角形的性质得出比例式,再利用比例的性质得出FD2=FG·FB即可. 试题解析:(1)的数量关系是. 理由如下: . 又, (SAS). . (2), . . ...
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目


 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.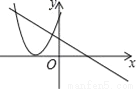 B.
B. 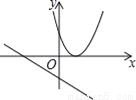 C.
C. 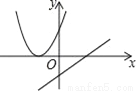 D.
D. 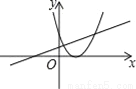
 B.
B.  C.
C.  D.
D. 
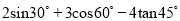 (2) 解方程:
(2) 解方程: 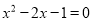
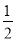 B.
B. 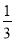 C.
C. 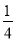 D.
D.