题目内容
 如图,△ABC中,AB=AC,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB上的一点,连接DG,交AE于点H,AG=2,DG=2,AD=2
如图,△ABC中,AB=AC,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB上的一点,连接DG,交AE于点H,AG=2,DG=2,AD=2| 2 |
(1)判断△AGD的形状;
(2)求证:GH是线段AB的中垂线;
(3)求证:AF=2HE.
考点:全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质
专题:
分析:(1)根据勾股定理的逆定理推出即可;
(2)求出AG=BG,即可得出答案;
(3)证△DAF≌△DBC,推出AF=BC,求出∠HBE=∠EHB=45°,求出HE=BE,即可推出答案.
(2)求出AG=BG,即可得出答案;
(3)证△DAF≌△DBC,推出AF=BC,求出∠HBE=∠EHB=45°,求出HE=BE,即可推出答案.
解答:(1)解:∵AG2+DG2=22+22=8=(2
)2=AD2
∴由勾股定理的逆定理得△ADG是等腰直角三角形;
(2)证明:∵△ADG是等腰直角三角形,
∴∠DAG=∠ADG=45°,∠AGD=90°.
∵BD⊥AC,
∴∠ADB=90°,
∠BDG=45°,
∴∠DBG=BDG=45°=∠DAB,
∴AG=BG,
∴GD是线段AB的中垂线;
(3)连结HB,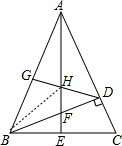
∵△ADG是等腰直角三角形;
∴∠DAG=45°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠ABD=∠DAB=45°,
∴DA=DB,
∵AB=AC,AE平分∠BAC
∴AE⊥BC,
∵BD⊥AC,
∴∠BDC=∠AEC=90°,
∴∠C+∠DAF=90°,∠C+∠DBC=90°,
∴∠DAF=∠DBC,
在Rt△BDC和Rt△ADF中,
,
∴Rt△BDC≌Rt△ADF (ASA),
∴BC=AF,
∵DG垂直平分AB,
∵点H在DG上,
∴HA=HB,
∴∠HAB=∠HBA=
∠BAC=22.5°,
∴∠BHE=∠HAB+∠HBA=45°,
∴∠HBE=∠ABC-∠ABH=67.5°-22.5°=45°,
∴∠BHE=∠HBE,
∴HE=BE=
BC,
∵AF=BC,
∴HE=
AF,
即AF=2HE.
| 2 |
∴由勾股定理的逆定理得△ADG是等腰直角三角形;
(2)证明:∵△ADG是等腰直角三角形,
∴∠DAG=∠ADG=45°,∠AGD=90°.
∵BD⊥AC,
∴∠ADB=90°,
∠BDG=45°,
∴∠DBG=BDG=45°=∠DAB,
∴AG=BG,
∴GD是线段AB的中垂线;
(3)连结HB,

∵△ADG是等腰直角三角形;
∴∠DAG=45°,
∵BD⊥AC,
∴∠ADB=90°,
∴∠ABD=∠DAB=45°,
∴DA=DB,
∵AB=AC,AE平分∠BAC
∴AE⊥BC,
∵BD⊥AC,
∴∠BDC=∠AEC=90°,
∴∠C+∠DAF=90°,∠C+∠DBC=90°,
∴∠DAF=∠DBC,
在Rt△BDC和Rt△ADF中,
|
∴Rt△BDC≌Rt△ADF (ASA),
∴BC=AF,
∵DG垂直平分AB,
∵点H在DG上,
∴HA=HB,
∴∠HAB=∠HBA=
| 1 |
| 2 |
∴∠BHE=∠HAB+∠HBA=45°,
∴∠HBE=∠ABC-∠ABH=67.5°-22.5°=45°,
∴∠BHE=∠HBE,
∴HE=BE=
| 1 |
| 2 |
∵AF=BC,
∴HE=
| 1 |
| 2 |
即AF=2HE.
点评:本题考查了全等三角形的性质和判定,线段垂直平分线的性质,勾股定理的逆定理,等腰三角形的性质,三角形内角和定理等知识点的应用,主要考查学生的推理能力,难度偏大.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
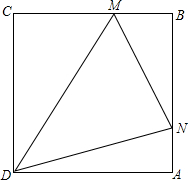 已知,边长为a(cm)的正方形ABCD,现有∠MDN=45°,其两边分别与CB、AB交与点M、N,连接MN,将∠MDN绕着顶点D旋转且使得M、N始终在边CB和边AB上,试判断在这一过程中,△BMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.
已知,边长为a(cm)的正方形ABCD,现有∠MDN=45°,其两边分别与CB、AB交与点M、N,连接MN,将∠MDN绕着顶点D旋转且使得M、N始终在边CB和边AB上,试判断在这一过程中,△BMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.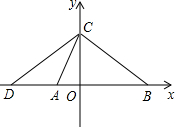 如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点C,过点C与AC垂直的直线交x轴于点B,在x轴负半轴上取一点D,使AD=OC,连接CD.
如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点C,过点C与AC垂直的直线交x轴于点B,在x轴负半轴上取一点D,使AD=OC,连接CD.