题目内容
【题目】已知:如图,点![]() 是以
是以![]() 为直径的
为直径的![]() 上一点,直线
上一点,直线![]() 与过
与过![]() 点的切线相交于
点的切线相交于![]() ,点
,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)详见解析;(2)![]() 的半径为6.
的半径为6.
【解析】
(1)连接CB、OC,根据切线得∠ABD=90°,根据圆周角定理∠ACB=90°,即∠BCD=90°,则根据直角三角形斜边上的中线性质得CE=BE,于是得到∠OBC+∠CBE=∠OCB+∠BCE=90°,然后根据切线的判定定理得CF是O得切线;
(2)CE=BE=DE=3,于是得到CF=CE+EF=4,然后根据相似三角形的性质即可得到结论.
(1)证明:连接![]() ,
,![]() ,
,
∵![]() 为
为![]() 的切线,
的切线,![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
∴![]() .
.
又∵![]()
∴![]() .
.
∴![]() .
.
∴![]() 是
是![]() 的切线.
的切线.
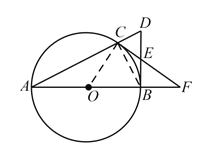
(2)解:∵![]() ,
,![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∴![]() ,即
,即![]() 的半径为6.
的半径为6.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目