题目内容
6. 如图所示,△ABC内接于⊙O,AB=100,∠ACB=45°,则⊙O的直径为( )
如图所示,△ABC内接于⊙O,AB=100,∠ACB=45°,则⊙O的直径为( )| A. | 50$\sqrt{2}$ | B. | 100$\sqrt{2}$ | C. | 150$\sqrt{2}$ | D. | 200$\sqrt{2}$ |
分析 连接OA、OB,根据圆周角定理,易知∠AOB=90°;因此△ABO是等腰直角三角形,可求出⊙O的半径,也就得出了⊙O的直径.
解答 解:连接OA、OB ,
,
∵∠ACB=45°,
∴∠AOB=90°,
∵OA=OB,
∴△ABO是等腰直角三角形,
∴AB=100,
∴AO=100×$\frac{\sqrt{2}}{2}$=50$\sqrt{2}$,
∴⊙O的直径=2AO=100$\sqrt{2}$,
故选B.
点评 本题考查了圆周角定理以及等腰直角三角形的判定和性质,得到△AOB是等腰直角三角形是解题关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 已知:如图,∠AOE=70°,OB、OD分别平分∠AOC,∠COE,求∠BOD的度数.
已知:如图,∠AOE=70°,OB、OD分别平分∠AOC,∠COE,求∠BOD的度数. 已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC. 如图,在Rt△ABC中,∠C=90°,∠B=30°,CD⊥AB于D点,DE⊥CB于E点.若AB=1,则DE=$\frac{3}{8}$.
如图,在Rt△ABC中,∠C=90°,∠B=30°,CD⊥AB于D点,DE⊥CB于E点.若AB=1,则DE=$\frac{3}{8}$.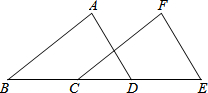 如图,点B、C、D、E在同一直线上,BC=DE,AB=FC,AD=EF.
如图,点B、C、D、E在同一直线上,BC=DE,AB=FC,AD=EF. 下图是从正面、上面看由一些大小相同的小正方体搭成的几何体得到的平面图形.
下图是从正面、上面看由一些大小相同的小正方体搭成的几何体得到的平面图形.