题目内容
15.$\sqrt{x+2y+1}$与|2x+y-3|是相反数,则x+y的平方根为±$\frac{\sqrt{6}}{3}$.分析 利用互为相反数两数之和为0列出关系式,利用非负数的性质得出方程组,求出方程组的解得到x与y的值,进而确定出x+y的平方根即可.
解答 解:∵$\sqrt{x+2y+1}$与|2x+y-3|是相反数,
∴$\sqrt{x+2y+1}$+|2x+y-3|=0,
∴$\left\{\begin{array}{l}{x+2y=-1①}\\{2x+y=3②}\end{array}\right.$,
②×2-①得:3x=7,即x=$\frac{7}{3}$,
①×2-②得:3y=-5,即y=-$\frac{5}{3}$,
∴x+y=$\frac{2}{3}$,
则x+y的平方根为±$\frac{\sqrt{6}}{3}$.
故答案为:±$\frac{\sqrt{6}}{3}$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
5.下列线段能构成直角三角形的是( )
| A. | 3,5,7 | B. | 5,7,8 | C. | 4,6,7 | D. | 5,12,13 |
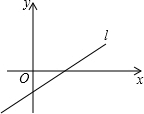 已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示.
已知直线l:y=(m-3)x+n-2(m,n为常数)的图象如图所示. 如图,已知一次函数y1=x+2与y2=-x的图象交于点A,请你在图中标明点A的坐标,并根据图象探讨:当x取什么值时,y1>y2.
如图,已知一次函数y1=x+2与y2=-x的图象交于点A,请你在图中标明点A的坐标,并根据图象探讨:当x取什么值时,y1>y2. 如图,平行四边形ABCD的4个内角平分线围成的四边形PQRS是矩形吗?说说你的理由.
如图,平行四边形ABCD的4个内角平分线围成的四边形PQRS是矩形吗?说说你的理由.