题目内容
6．
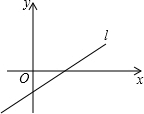已知直线l：y=（m-3）x+n-2（m，n为常数）的图象如图所示．（1）求m、n的取值范围；
（2）化简|m-n|-$\sqrt{{n}^{2}-4n+4}$-|m-2|．
分析 （1）根据直线的增减性和与y轴的交点的位置确定两个未知数的取值范围即可；
（2）根据确定的m、n的取值范围去掉绝对值符号进行化简即可．
解答 解：（1）∵图象与y轴交与负半轴，y随着x的增大而增大，
∴$\left\{\begin{array}{l}{m-3＞0}\\{n-2＜0}\end{array}\right.$，
解得：m＞3，n＜2；
（2）∵m＞3，n＜2，
∴m-n＞0，
∴原式=m-n-2+n-m+2=0．
点评 本题考查了一次函数的图象与系数的关系，解题的关键是根据增减性及与坐标轴的交点情况确定两个待定系数的取值范围，难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
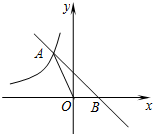如图，直线y=-x+b与双曲线$y=-\frac{1}{x}$（x＜0）交于点A，与x轴交于点B，则OA2-OB2=（ ）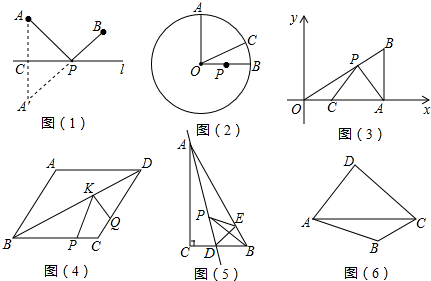
如图，平行四边形ABCD中，AC与BD相交于点O，猜想OA与BD的关系．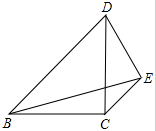
如图，等腰直角△BCD中，BC=CD，E是边CD外的一点，且CE∥BD，BE=BD，则CE：BD的值$\frac{\sqrt{3}-1}{2}$．